|
|
|
\require{AMSmath}



Eigenschappen bewijzen met behulp van de middenparallel
Hoe bewijs dat een vierhoek een paralellogram is met behulp van de middenparallel?
boris
Overige TSO-BSO - zondag 21 maart 2004
Antwoord
Dag Boris,
Je bedoelt dus:
De middens van de zijden van een vierhoek zijn de hoekpunten van een parallellogram.
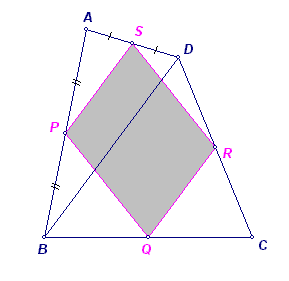
We moeten dus bewijzen dat in bovenstaande figuur PQRS een parallellogram is.
We tekenen de diagonaal BD van ABCD.
De lijn PS is dan de zogenoemde 'middenparallel' van driehoek ABD.
En van PS weten we twee dingen:
__(1) PS = 1/2 BD
__(2) PS // BD
Als je deze beide eigenschappen niet kent, dan kan je ze, denk ik, bewijzen door te kijken naar de (gelijkvormige) driehoeken APS en ABD.
En dan.
Kijk nu ook eens naar QR en BD.
Welke twee zaken weten we (nu ook) van die twee lijnstukken? Vul in:
__(3) ... = ...
__(4) ... // ...
En dan is de conclusie niet ver meer.
We weten dan, kijkend naar PS en QR (en vul weer in):
__(5) PS = ...
__(6) PS // ...
Oja, de stelling, dat een vierhoek een parallellogram is, als je weet dat twee zijden evenwijdig zijn en gelijk aan elkaar, ken je natuurlijk!
Overigens, het parallellogram PQRS heet Varignon-parallellogram van vierhoek ABCD.
Succes!
Nagekomen (op 12-04-05)
Deze bewijsvoering gaat overigens ook op als de verhoudingen
|AS|:|AD| , |AP|:|AB| , |CQ|:|CB| , |CR|:|CD|
hetzelfde zijn, omdat dan ook de driehoeken gelijkvormig zijn.
(Met dank aan USS.)

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 21 maart 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










