WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Afgeleide cirkel, bol en cilinder

Hallo,

Waarom is de omtrek van een cirkel de afgeleide van de oppervlakte van een cirkel; namelijk. oppervlakte = $\pi$r²;
opp' = 2$\pi$r (dus de omtrek)
Zelfde geld voor een bol. inhoud bol $\frac{4}{3}\pi$r³, afgeleiden daarvan is 12/3$\pi$r² dus. 4$\pi$r². Wat is de theorie daarachter
Pieter
Leerling bovenbouw havo-vwo - maandag 15 maart 2004

Antwoord

Hallo Pieter,

ik zal je vraag uitleggen voor een cirkel, voor een bol werkt het in feite precies hetzelfde, maar dat wordt wat meer tekenwerk in 3D. De oppervlakte van een cirkel kun je berekenen door integratie:

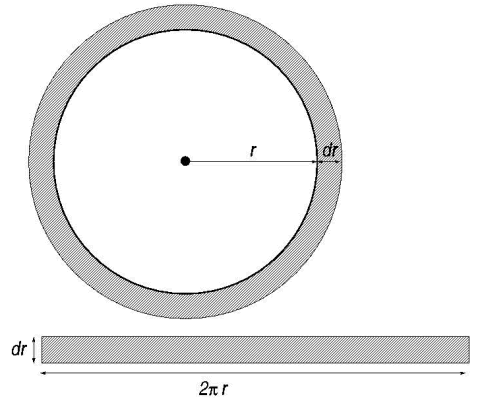
Stel je hebt een cirkel met straal r en voegt daar een heeeeeel dun schilletje met dikte dr aan toe tot een nieuwe cirkel met straal r+dr (in het plaatje overdreven groot weergegeven). Hoeveel oppervlakte komt er dan bij?

Welnu, als je het strookje loshaalt en recht uitspant, dan kun je de oppervlakte berekenen als breedte maal hoogte. De breedte is dan de omtrek van de cirkel 2$\pi$r en de hoogte is dr (hierbij is het belangrijk dat de straal loodrecht op de omtrek van de cirkel staat). Dit is natuurlijk niet helemaal waar, omdat de omtrek en dus de breedte van het strookje groeit met de afstand tot het middelpunt, maar als je dr maar klein genoeg neemt, dan klopt het steeds beter en in de limiet is het OK. Nu is de totale oppervlakte van de cirkel de som van al deze kleine beetjes. In de limiet voor infinitesimaal kleine dr is dit per definitie de integraal, dus:

$\int{}$ omtrek dr = oppervlakte

Dit is nog niet helemaal een goed bewijs (voor een wiskundige op de universiteit tenminste niet ) omdat je nog moet bewijzen dat de fout inderdaad naar nul gaat in de limiet voor dr$\to$0. Een bewijs dat helemaal op alle details ingaat is echter wat te ingewikkeld om hier weer te geven. Ik hoop dat je tevreden zult zijn met dit antwoord.

Guido Terra

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 16 maart 2004