WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Goniometrische getallen van verwante hoeken

hoe vereenvoudig ik sin(90°-alfa)*tan(180°-alfa)
draris
Overige TSO-BSO - woensdag 10 maart 2004

Antwoord

Hoi,

Ik ga je dit uitleggen a.d.h.v. de eenheidscirkel (de goniometrische cirkel, da's een cirkel met middelpunt (0,0) en straal 1).
We gaan eerst sin(90°-a) vereenvoudigen, en daarna tan(180°-a) en dan kijken we of we het product nog verder kunnen vereenvoudigen.

sin(90°-a)

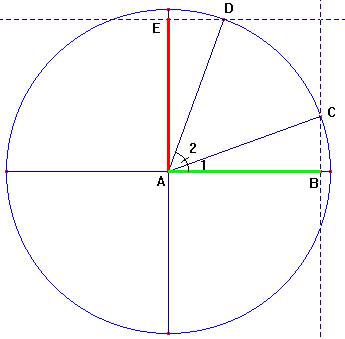
De hoek a is gelijk aan hoek BAC (waar het 1'tje in staat). Een hoek van 90° wordt gevormd door het groene en het rode lijnstuk, maar we moesten 90°-a hebben dus ga je nog a° terug (met de klok mee) dan kom je uit op het punt D (dit is de hoek BAD waar je het 2'tje ziet staan).
Om te weten wat de cosinus van een hoek is projecteer je het snijpunt van de goniometrische cirkel op de horizontale as. De cosinus van hoek a vind je dus als volgt: je ziet dat de goniometrische cirkel gesneden wordt in het punt C vanuit dit punt trek je een loodlijn op de horizontale as (=projecteren op de horizontale as, het punt B is de projectie van C) en het afgesneden stuk (groen gekleurd) is de cosinus van die hoek. Dus cos(a) = |AB|.

Om te weten wat de sinus van een hoek is projecteer je het snijpunt van de goniometrische cirkel op de verticale as. De sinus van hoek 90°-a vind je dus door vanuit het punt D (daar wordt de cirkel gesneden) een loodlijn op de verticale as neer te laten, in het punt E. De afstand |AE| is de sinus van die hoek. Dus sin(90°-a) = |AE|.

Wat valt je op? Het rode lijnstuk is even lang als het groene, dus is sin(90°-a) = cosa. Probeer hetzelfde nog eens in de andere kwadranten.

tan(180°-a)

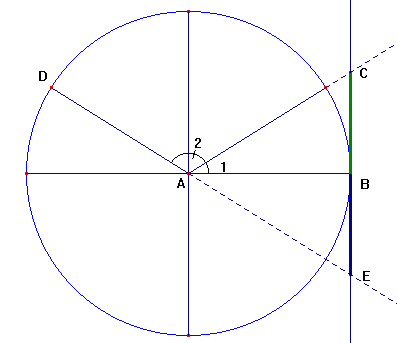
(Voor de overzichtelijkheid heb ik de hoek a wat groter getekend, maar in werkelijkheid is deze even groot als in de vorige tekening).

Hoek a wordt wederom gevormd door hoek BAC (zie 1'tje) en hoek 180°-a wordt gevormd door eerst een gestrekte hoek te tekenen en daarna a° terug draaien (met de klok mee, snijpunt met goniometrische cirkel is D).

Om te weten wat de tangens is moet er een zogeheten tangensas getekend worden, die is evenwijdig aan de verticale as en gaat door het punt (1,0). De tangens van hoek a heb ik aangegeven met het groene lijnstuk (het punt C snijdt de tangensas. Alles boven het punt B (het punt B heeft als coördinaten (1,0)) is positief, alles onder het punt B is negatief en het punt B zelf is 0. Dus de tangens van hoek a is positief (in dit geval!!). De tangens van 180°-a heb ik aangegeven met het blauwe lijnstukje (|BE|). Aangezien deze onder de B ligt is de tangens hiervan negatief. Verder zie je dat het groene en het blauwe lijnstukje even lang zijn, maar tegengesteld zijn. Dus tan(a) = -tan(180°-a) oftwel tan(180°-a) = -tan(a).

Dus gecombineerd wordt sin(90°-a)·tan(180°-a) = cos(a)·-tan(a). We mogen die min ook van voor zetten, dan krijgen we -cos(a)·tan(a).
Maar we weten ook dat tan(a) = ^sin(a)/_cos(a) Þ -cos(a)·^sin(a)/_cos(a) en dan mogen we die cosinussen wegstrepen waardoor je -sin(a) krijgt.

Dus sin(90°-a)·tan(180°-a) = -sin(a).

Groetjes,

Davy.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 10 maart 2004