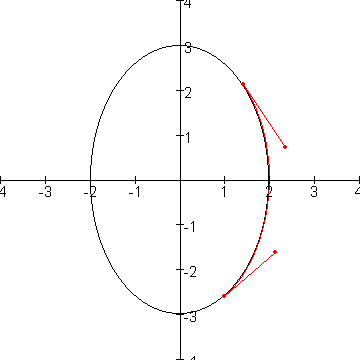WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Element van ellips construeren met een Bezier-kromme

Dit is een reactie op vraag 20836

Voor de duidelijkheid, een raaklijn aan een ellips op punt (x₁,y₁) is:

x·x₁/a² + y·y₁/b²=1

Ik begrijp niet goed hoe je dan een bezier curve zou moeten maken die de Ellips wel volgt. Stel dat ik twee controlepunten zou moeten bepalen, hoe bepaal ik die dan?
Joel d
Student universiteit België - dinsdag 2 maart 2004

Antwoord

Het leuke van die bezierkrommen is het volgende:
als je de (b.v. 4) punten die de kromme aan een gelijkvormigheidstranformatie onderwerpt bijgevolg de hele kromme aan dezelfde gelijkvormigheidstransformatie onderwerpt.
Een ellips met halve as a in de x-richting en halve as b in de y-richting ontstaat door een cirkel met straal 1 horizontaal te vermenigvuldigen met a en verticaal met b.

Eerst heb ik uitgezocht hoe je een cirkelsegment tussen twee punten A en B kunt benaderen met een bezierkromme:

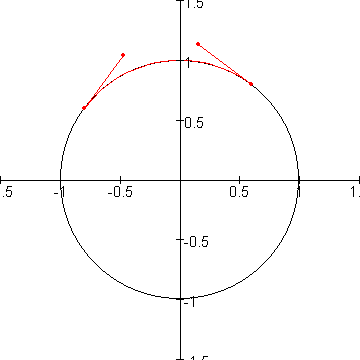
Het hiervoor gebruikte programmaatje volgt (met wat commentaar) hieronder:

a1:=0.6
a2:=sqrt(1-a1^2)
b1:=-0.8
b2:=sqrt(1-b1^2)
%tercontrole cirkel met straal 1 tekenen
cirkelmppunt(0;0;a1;a2)
%bereken de cosinus cd van de hoek AOB
cd:=a1*b1+a2*b2
%bereken nu de sin en cos van 0.5(hoek AOB)
sa:=sqrt(0.5-0.5*cd)
ca:=sqrt(0.5+0.5*cd)
%f is de gezochte vermenigvuldig factor
f:=(1-ca)/0.75/sa
%C is controle punt bij A
c1:=a1-f*a2
c2:=a2+f*a1
%D is controle punt bij B
d1:=b1+f*b2
d2:=b2-f*b1
tekenkleur(255)
bezier(a1;a2;c1;c2;d1;d2;b1;b2)
stip(a1;a2;2)
stip(b1;b2;2)
stip(c1;c2;2)
stip(d1;d2;2)
lijn(a1;a2;c1;c2)
lijn(b1;b2;d1;d2)

Een paar kleine probleempjes: de cirkelboog moet niet groter zijn dan 180°, en de twee punten moeten in de juiste volgorde worden opgegeven.
Waarom dit een redelijke benadering is kun je afleiden uit de eigenschappen van een cirkel en zijn raaklijnen + de eigenschappen van een bezierkromme met 2 controlepunten.
Eventueel wil ik dat wel toelichten, maar ik weet niet of je daar behoefte aan hebt.

Hoe doe je het nu met een ellips?
Eerst voer je op de gegeven punten twee lijnvermenigvuldigingen uit zodat je de bijbehorende punten op een eenheidscirkel krijgt.
Daarna berekeningen uitvoeren en weer terugvermenigvuldigen.

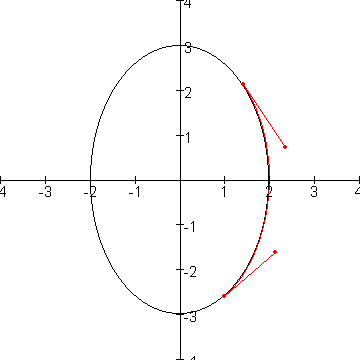
Hieronder het gebruikte programmaatje:

%de halve assen van de ellips zijn a en b
a:=2
b:=3
%P en Q zijn de gegeven punten op de ellips
p1:=a*cos(-1/3*pi)
p2:=b*sin(-1/3*pi)
q1:=a*cos(1/4*pi)
q2:=b*sin(1/4*pi)
%ter controle ellips tekenen
ellips(-a;-b;a;b)
Terugrekenen naar de eenheidscirkel
a1:=p1/a
a2:=p2/b
b1:=q1/a
b2:=q2/b
%nu de berekeningen voor de eenheidscirkel
cd:=a1*b1+a2*b2
sa:=sqrt(0.5-0.5*cd)
ca:=sqrt(0.5+0.5*cd)
f:=(1-ca)/0.75/sa
%controlepunten berekenen en terug naar ellips
c1:=(a1-f*a2)*a
c2:=(a2+f*a1)*b
d1:=(b1+f*b2)*a
d2:=(b2-f*b1)*b
tekenkleur(255)
bezier(p1;p2;c1;c2;d1;d2;q1;q2)
stip(p1;p2;2)
stip(q1;q2;2)
stip(c1;c2;2)
stip(d1;d2;2)
lijn(p1;p2;c1;c2)
lijn(q1;q2;d1;d2)

De programmaatjes zijn geschreven in het tekenprogramma wiskit maar ik hoop dat je ze vrij eenvoudig kunt omzetten naar een andere programmeertaal.
De opmerking over die gelijkvormigheidstransformaties geeft verder voldoende stof om ook ellipsen met assen niet evenwijdig aan de coordinaatassen bij benadering te kunnen tekenen.
Succes!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 3 maart 2004