WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Sin en cos

Sorry van de tweede vraag ik had ff iets beter moeten kijken.
Bij c) komt er bij mij a=4,07 uit
en bij d) komt er a=3,79 uit maar deze antwoorden moeten omgdraaid worden.
Volgens mij snap ik niet zo goed hoe dat met de eenheidscirkel werkt, zou je dat misschien een beetje willen uitleggen. Dank je
Fleur
Leerling bovenbouw havo-vwo - zondag 22 februari 2004

Antwoord

Hoi Fleur,

Natuurlijk, geen probleem.
De eenheidscirkel is een hulpmiddeltje bij goniometrie.
Teken hiervoor een cirkel met straal 1.

Eerst nog even een klein uitstapje... De omtrek van een cirkel bereken je altijd met omtr. = 2·$\pi$·r, in dit geval is dat dus precies 2$\pi$. Waarom wordt dit erbij gehaald, vraag je je misschien af, maar de sin en cos herhalen zichzelf beide met periode 2$\pi$. Bij ¹/₄ van de omtrek, dus waar de cirkel de (positieve) y-as snijdt, hoort dus ¹/₂$\pi$. Evenzo hoort halverwege de cirkel (snijpunt met negatieve x-as) de waarde $\pi$, op ³/₄ hoort dan 1¹/₂$\pi$ en aan het einde de waarde 2$\pi$ oftewel 0 (vanwege de periodiciteit!).

Het 'handige' van een eenheidscirkel is, dat als je het punt op de eenheidscirkel pakt de bijbehorende x-waarde precies de cosinus van dit getal is en de bijbehorende y-waarde de sinus van dit getal is.
Neem bijvoorbeeld 0,5$\pi$ op de cirkel, dit is het punt (0,1). Dus cos 0,5$\pi$ = 0 en sin 0,5$\pi$ = 1

Nu switchen we even naar jouw vraag, opgave c:
sin $\alpha$=-0,6 en $\pi$$<$$\alpha$$<$1,5$\pi$
De cirkel heeft op 2 punten de y-waarde -0.6, zie de tekening hieronder. Nl de snijpunten van de rode lijn (y=-0.6) met de cirkel. De waarde die je rekenmachine geeft is standaard de waarde die het dichtst bij 0 ligt, in dit geval dus de waarde bij het meest rechtse punt in het 4e kwadrant. Het andere punt is dus (kijk in je tekening...) $\alpha$=$\pi$+0.645... =3.79.

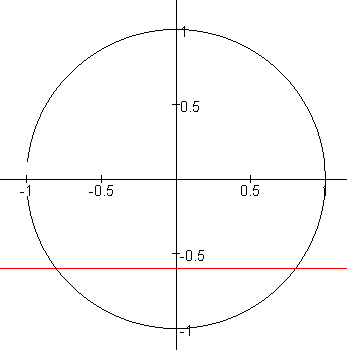
Opgave d gaat op dezelfde wijze. De cosinus komt overeen met de x-as. Kijk dus waar de cirkel de x-waarde -0.6 heeft. Welke waarde geeft je rekenmachine, in welk kwadrant ligt dit antwoord en in welk kwadrant moet het antwoord liggen, wat is dan het antwoord?

Succes weer

Erica

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 22 februari 2004