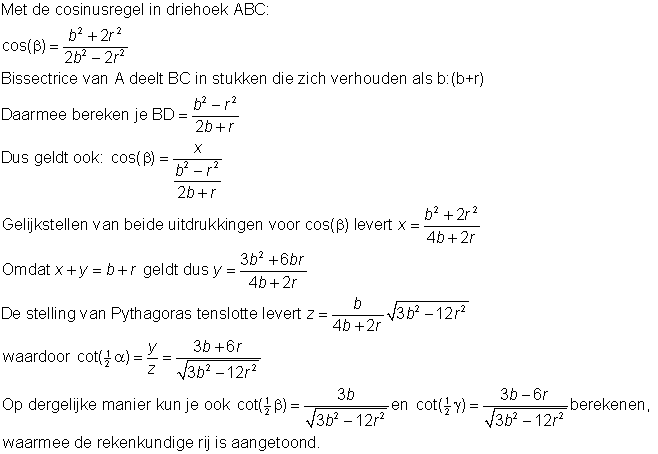WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Rekenkundige rij van cot

Hallo,

gegeven is dat a, b en c zijden zijn van een driehoek en een rekenkundige rij vormen. Te bewijzen valt nu dat :

cot (a/2) , cot (b/2) , cot (g/2) ook een rekenkundige rij vormen.

ik stelde dat je om van cot (a/2)naar cot (b/2) te gaan dus een getal V moest optellen, idem om van cot (b/2) naar cot (g/2)te gaan (dit noemde ik V2)

dan geldt :
V1 = cot (b/2)- cot (a/2)
V2 = cot ( g/2) - cot (b/2)

als V1 gelijk is aan V2 dan hebben we dus een rekenkundige rij.

na enig rekenwerk kom ik dan terecht bij iets dat er begint op te lijken :

V1=V2

Û

cot (b/2) =(1/2.cos (b/2))/(sin(g/2).sin(a/2))

hoe los je dit nu op ? Alvast bedankt.
Pieter
3de graad ASO - vrijdag 13 februari 2004

Antwoord

Tjonge, dat is best ingewikkeld.
Ik weet niet of er elegantere oplossingen mogelijk zijn, maar ik kom niet verder dan stug rekenwerk.
Ik begin iets anders dan dat jij suggereert.
Ik neem als variabelen:
b (de lengte van zijde b), en
r ( het verschil van b en a, en dus ook het verschil van c en b)
Dus a=b-r, en c=b+r.

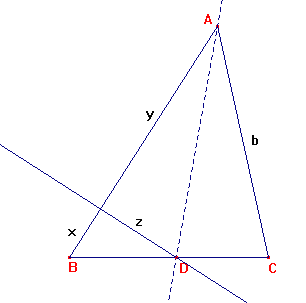
Nu ga ik cot(¹/₂a) ook uitdrukken in b en r.

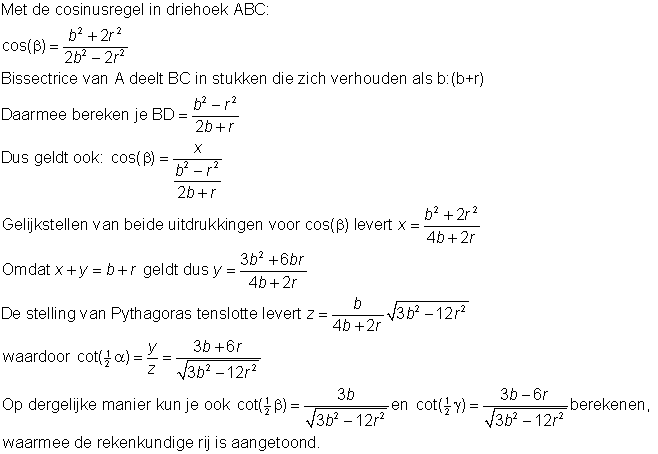
Ik hoop dat dit de bedoeling was, anders hoor ik het graag!

PS: van collega-beantwoorder Dick (ik had het kunnen weten...) kwam de volgende elegante oplossing:
Noem de hoeken even 2A, 2B en 2C (dan hoef je niet met halven te werken)
en de zijden a, a+p, a+2p
s is de halve som van de zijden.
r is de straal van de ingeschreven cirkel.
Dan geldt

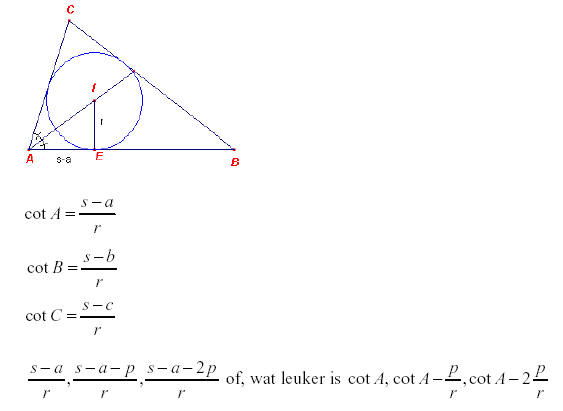
groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 16 februari 2004