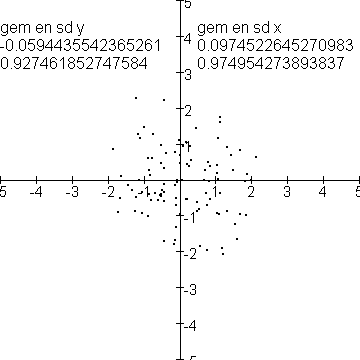WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Verwachting

Als je een random walk wilt maken waarbij je de stapjes maakt op basis van een getrokken hoek uit een bepaalde verdeling, en elke nieuwe hoek is de vorige getrokken hoek plus een nieuw getrokken getal uit de verdeling met verwachting nul.
De allereerste stap leg je op in de positieve x-richting. Wat is dan de verwachting voor X na n stappen?

Wij hebben tot nu toe dat de verwachting van x voor de tweede stap gelijk is aan E(X) = cos(E(hoek)). Voor de stap hierna krijgen we: E(X) = cos(vorige hoek)+cos(E(hoek)). Dit kun je zo herhalen voor n stappen, maar E(hoek) = 0, dus uiteindelijk komen we dan op totaal(E(X)) = n*stapgrootte. Dit betekent dus dat de verwachting is dat de random walk helemaal een rechte lijn is, maar dit lijkt ons toch ook weer onwaarschijnlijk. Wat doen we fout, of klopt dit zo?
Ernst-
Student universiteit - donderdag 12 februari 2004

Antwoord

Uit E(hoek)=0 mag je niet concluderen dat E(cos(hoek))=cos(E(hoek))=cos(0).
De fout zit hierin dat niet algemeen geldt E(f(X))=f(E(X)).
Verder heb je het zomaar oer een verdeling met verwachting nul. Zeker als je daar een cosinus van neemt maakt het natuurlijk wel even iets uit hoe die verdeling dan verder is: normaal (wat is sigma), blok (wat is het domein).
Om je te overtuigen heb ik maar eens even wat gesimuleerd:

Ik heb als verdeling genomen: gewone random getallen tussen -180 en 180.
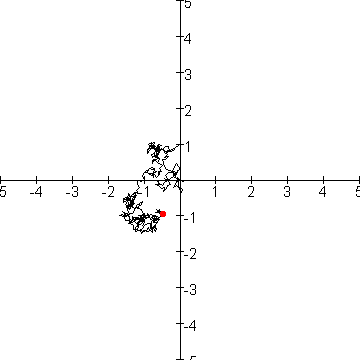
Hieronder zo'n random walk bestaande uit 200 stappen. Het eindpunt is met een rode stip aangegeven.

Hieronder de eindpunten van 99 van die random walks.
Bovendien gemiddelde en standaarddeviatie van de x'en en y'en van deze eindpunten.

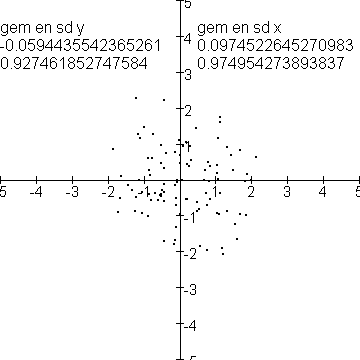
Deze simulaties zijn gemaakt met het programma Wiskit
Leuk om verder mee te experimenteren.
De eerste tekening met het programma:
dx:=0.1
x:=0
y:=0
for(i;1;200;1)
a:=rnd(360)-180
nx:=x+dx*cos(degtorad(a))
ny:=y+dx*sin(degtorad(a))
lijn(x;y;nx;ny)
x:=nx
y:=ny
L1(j):=x
L2(j):=y
next
tekenkleur(255)
stip(x;y;3)

De tweede met het programma:
dx:=0.1
for(j;1;99;1)
x:=0
y:=0
for(i;1;200;1)
a:=rnd(360)-180
nx:=x+dx*cos(degtorad(a))
ny:=y+dx*sin(degtorad(a))
x:=nx
y:=ny
L1(j):=x
L2(j):=y
next
stip(x;y;1)
next
stats(L1;1;99;gemx;sdx)
stats(L2;1;99;gemy;sdy)
tekst(0.5;4.5;gem en sd x)
uitvoer(0.5;4;gemx)
uitvoer(0.5;3.5;sdx)
tekst(-5;4.5;gem en sd y)
uitvoer(-5;4;gemy)
uitvoer(-5;3.5;sdy)

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 12 februari 2004