WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Functie bepalen

Kan je hier een functie uithalen of is dit enkel mogelijk bij benadering? En hoe bepaal ik die best? Als 4de graadsfunctie of als exponentiele functie of hoe? Groetjes

x Y
-20 14616
-10 8941
0 5634
10 3652
20 2431
30 1657
40 1154
50 819
60 592
70 434
80 324
90 246

Jan Le
Iets anders - woensdag 11 februari 2004

Antwoord

In principe kun je van elk van dit soort getallenrijtjes een exact functievoorschrift maken, als je maar genoeg coëfficiënten meeneemt.
Bijvoorbeeld kun je hier exact een elfdegraads functievoorschrift bij maken, waarbij de waarden precies overeenkomen.
Als je kolommen 87 getallen zouden bevatten, kun je dit met een 86-e graads functie exact beschrijven.
Maar:
dat is natuurlijk niet zo zinvol.

Je kunt beter een benaderend functievoorschrift zoeken.
Een grafiek, bijvoorbeeld in Excel, kan je op een idee brengen, zeker als je eens probeert om op een of beide assen een logaritmische toe te passen.
In jouw geval blijkt bij logaritmische y-as de grafiek praktisch een rechte lijn te zijn.
Dat betekent dat het oorspronkelijke verband exponentieel zou kunnen zijn.

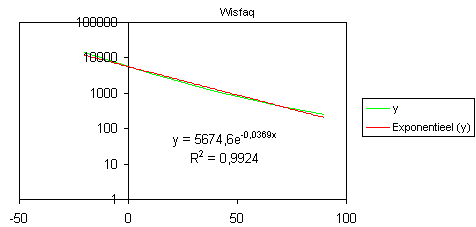
Een exponentiële trendlijn geeft een correlatie R=0.9924, dus dat is behoorlijk goed. (Hoe dichter bij 1, hoe beter)
Maar je kunt wel zien dat er aan de uiteinden een duidelijke afwijking van de rechte lijn optreedt.
Daarom proberen we ook nog een vierdegraads trendlijn:

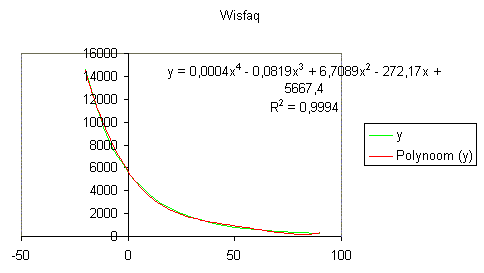
Je ziet dat R nog beter is.
Conclusie kan zijn: ga voor de vierdegraadsbenadering.
Maar het valt niet mee om hier absolute uitspraken over te doen.
Ik hoop dat je hiermee geholpen bent.
groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 11 februari 2004

Re: Functie bepalen