WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Spiegelen

Ik ben 13 jaar en ik heb moeite met spiegelen. Hoe kan ik goed zien of ik het goed doe zijn er ezelsbruggetjes voor of iets anders?
sebast
Leerling onderbouw vmbo-havo-vwo - dinsdag 10 februari 2004

Antwoord

Dag Sebastiaan,

Oei, hoe moet ik je daar nu bij helpen...

Allereerst maar een klein beetje theorie. Spiegelen doe je met een spiegelas: een rechte lijn (s). Elk punt P heeft een spiegelbeeld, en de afstand van het spiegelbeeld tot de spiegelas is gelijk aan de afstand van P tot die spiegelas.
Dit kan je zien in onderstaande figuur (voor een punt P, een lijnstuk XY en een driehoek ABC).
De rode figuren zijn de spiegelbeelden van de zwarte, EN ook: de zwarte figuren zijn de spiegelbeelden van de rode.

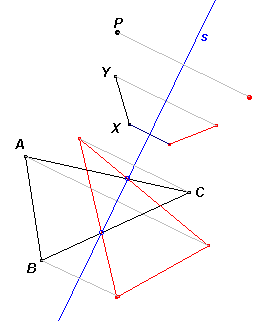
Een ezelsbruggetje: ligt een figuur aan weerskanten van de spiegelas, dan snijden de figuur en z'n spiegelbeeld elkaar OP de spiegelas (zie de driehoek).
Ook: als je het lijnstuk XY langer zou maken, en ook z'n spiegelbeeld, dan vind je het snijpunt weer op s.
In de onderstaande applet staat een driehoek ABC en z'n (rode) spiegelbeeld in de lijn s.

Applet werkt niet meer.
Download het bestand.

Je kan de lijn s verplaatsen met het punt X (punt aanwijzen met je muis en dan slepen). Door het punt Y te draaien over het cirkeltje kan je de spiegelas draaien om X. Kijk maar eens wat er gebeurt.

Maar er is meer. Je kan ook de driehoek zelf verplaatsen (aanwijzen, je ziet 'Deze driehoek', en slepen).
Ook de vorm van de driehoek kan je veranderen door alleen een punt, A, B of C, te verslepen. Je ziet dan dat het spiegelbeeld telkens mee verandert. Kijk daarbij naar de snijpunten (ezelsbrug) op de spiegelas!

Je kan de driehoek ook veranderen in een parallellogram (schuif de knop
Probeer dat ook eens met het parallellogram...
Laat bijvoorbeeld de lijn s samenvallen met de diagonaal AC van het parallellogram. En verplaats dan het punt B eens om de beide figuren te laten samenvallen (Dat kan!)
Herken je dan de figuren waarbij dat mogelijk is (wat zijn het voor soort figuren?). Hoe moet je punt B dan verschuiven?

Maak van het parallellogram ook eens een rechthoek (ongeveer dan) en kijk eens hoe je de lijn s moet plaatsen om de figuren te laten samenvallen (op hoeveel manieren kan dat?)

Ik hoop dat dit je een beetje op weg helpt.
Succes!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 11 februari 2004