WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Trapezium

Hio een vraagje.
Stel ABCD een trapezoide met basis [AB].
Stel E en F twee punten op (AD) en (BC) zodat: EA/ED=FB/EC=K
Noem [CD] = b en [AB] = a. Druk EF uit in a,b en k.
Liner
Leerling onderbouw vmbo-havo-vwo - dinsdag 10 februari 2004

Antwoord

Hio!

We gaan er maar vanuit dat je een trapezium bedoelt, want dat is de naam die in het Nederlands wordt gebruikt voor wat ze in het Amerikaans een 'trapezoid' noemen.
En ik neem aan, dat EC (in je vraag) een typfoutje is (moet zijn FC?).
Uit het feit dat in dit geval EA/ED = FB/FC = k, kunnen we afleiden, dat EF evenwijdig is met AB (en CD).
We tekenen nu de lijn CHG evenwijdig met DA (H op EF, G op AB).

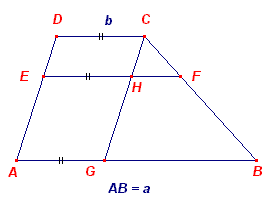
Uit FB/FC = k vinden we: FB = k.FC, zodat
CB = FC + FB = FC + k.FC = (1+k).FC
Maar omdat de driehoeken CHF en CGB gelijkvormig zijn, geldt ook:
GB = (1+k).HF of HF = GB/(1+k)
En dan:
EF = EH + HF = b + (a-b)/(1+k)
En in het rechter lid van deze uitdrukking staan nu alleen a, b en k.

N.B.
Wat kan je zeggen van de punten E en F als k = 1?
Kan je dan een eenvoudige uitdrukking vinden voor EF?
EF heet in dit geval wel 'middenparallel' van het trapezium.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 10 februari 2004