WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hyperbool construeren met behulp van twee cirkels

Hoe kan ik een hyperbool construeren met twee gegeven cirkels c1 en c2, met straal r1 en r2? Ik wil geen gebruik maken van de mogelijkheid om een derde cikel met straal r2-r1 of r1-r2 te construeren in een van de gegeven cirkels.
Esther
Leerling bovenbouw havo-vwo - woensdag 4 februari 2004

Antwoord

Misschien is het nuttig het probleem eerst wat preciezer vast te leggen.

Je wilt dus de conflictlijn tekenen van twee cirkelvormige gebieden:
Gebied 1 met middelpunt M en straal r₁;
Gebied 2 met middelpunt N en straal r₂.
Onder bepaalde voorwaarden is deze conflictlijn een hyperbool (welke?)

Kennelijk is behandeld/afgeleid dat je dit probleem kunt herleiden tot: de conflictlijn van een cirkel met een straal |r₁-r₂| en een punt.
Voor het construeren van punten van deze conflictlijn kun je onderstaande (cabri-)constructie gebruiken:

Applet werkt niet meer.
Download het bestand.

Je wilt nu hier geen gebruik van maken.
Een oplossing is dat je de een groot aantal isolijnen van beide cirkels tekent en de snijpunten van de isolijnen 'met gelijk nummer' door een vloeiende kromme verbindt.

Ik heb dat met het programma Wiskit voor je getekend:

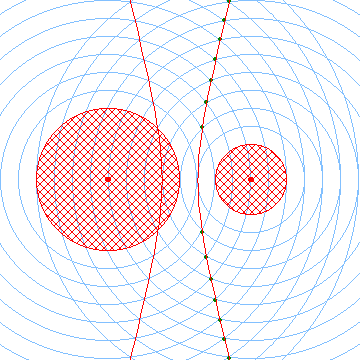
Ook heb ik de conflictlijn getekend volgens de manier die je niet wilde hebben.

Interessante vraag: welke voorwaarde moet je aan de nummers van de isolijnen stellen om de hyperbooltak te krijgen die je nu juist niet wilt hebben? Heeft dat wel of niet iets te maken met de stralen van beide cirkels?

Hieronder het gebruikte Wiskitprogramma:
assen=geen
maakpunt(m;-2;0)
maakpunt(n;2;0)
r₁:=2
r₂:=1
for(i;0.5;5;0.5)
tekenkleur(16760962)
cirkelmppunt(m1;m2;m1+r₁+i;m2)
cirkelmppunt(n1;n2;n1+r₂+i;n2)
snijpuntcircir(m1;m2;m1+r₁+i;m2;n1;n2;n1+r₂+i;n2;s;t)
tekenkleur(32768)
stip(s1;s2;2)
stip(t₁;t₂;2)
next
tekenkleur(255)
stip(m1;m2;3)
stip(n1;n2;3)
vulkleur(255)
vulstijl(7)
cirkelmppunt(m1;m2;m1+r₁;m2)
cirkelmppunt(n1;n2;n1+r₂;n2)
conflictlijn(cirkel;n1;n2;m1;m2;m1+r₁-r₂;m2)

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 4 februari 2004

Re: Hyperbool construeren met behulp van twee cirkels