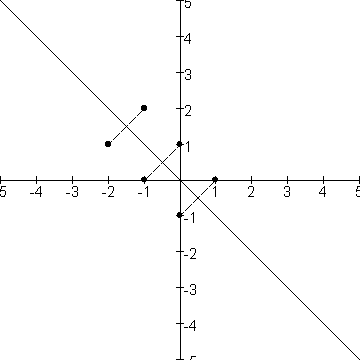WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Lineaire transformatie

Ik heb de volgende vraag:

T:²®² first performs a horizontal shear that transforms e2 into e2-2e1(leaving e1 unchanged) and then reflects points through the line x2=-x1. Find the standard matrix of T.

Zouden jullie deze som stap voor stap kunnen toelichten (het liefst met plaatjes), want ik kan me hier dus totaal geen voorstelling van maken.

Alvast bedankt!

Jacque
Student universiteit - zondag 1 februari 2004

Antwoord

De transformatie T is opgebouwd uit twee transformaties A en B die achtereenvolgens worden uitgevoerd.
A beeldt e2 af op e2-2e1=[-2 1], en e1 op e1=[1 0]
Deze twee vectoren zijn juist de kolomvectoren van A, dus A heeft de transformatiematrix

B is de spiegeling in de lijn: x2=-x1. Bij deze spiegeling kun je met een schetsje makkelijk inzien dat het beeld van e1 -e2=[0 -1] is en het beeld van e2 -e1=[-1 0] is. B heeft dus als transformatiematrix:

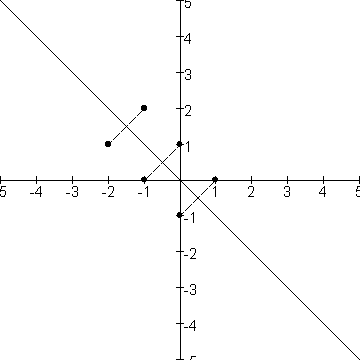
Je kunt het eindantwoord nu vinden door B.A uit te rekenen.
Het antwoord is

.
Je kunt dit ook zo inzien

Het beeld van e1=[1 0] is onder A: [1 0]. Het beeld hiervan onder B is [0 -1].
Het beeld van e2=[0 1] is onder A: [-2 1]. Het beeld hiervan is onder B [-1 2]
Hieruit volgt weer de matrix

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 1 februari 2004