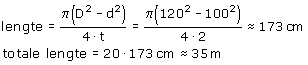WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Lengte meerdere spiralen bereken

Beste beantwoorder,

Voor ons Profielwerkstuk maken wij een magneetzweeftrein.
Nu moeten voor het wiskundide deel de lengte van draad op een spoel bereken.

Het idee van spoel is een kern met dikte. Daarom wind je draad, waardoor een winding onstaat en draai je meerder windingen naast elkaar. Op deze laag begin je op nieuw. Met dus een grotere straal.

Dit kan je natuurlijk op meerdere manier doen.
Simpel door de omtrek te nemen maal het aantal windingen en dan de omtrek weer opnieuw bereken maal het aantal windingen. Dit doe je tot je alle lagen hebt gehad.

Je hebt hier varianten op dus bijvoorbeeld de gemiddelde omtrek te nemen.

Maar wat nu onze vraag is, is het mogelijk, en zoja hoe. Om 1 formule te vinden die dit het beste benaderd en dit dan in wiskundige hoek van spiralen?

Wij willen verschillende methodes omdit te bereken vergelijken.

Wij zelf zaten te denken aan combinatie van een helix met de spiraal van pythagoras. Of de oppervlakte berekenen van een spiraal die breed is en dus meerdere lagen voorsteld. Soort van wenteltrap zonder treden. Maar we weten niet of dit een goede beredenering is voor de lengte.

Hier vindt u misschien wat meer uitleg:
http://mathworld.wolfram.com/ArchimedesSpiral.html

Bij deze formule voor de lengte kunnen wij de h in sinh^-1 niet plaatsen. Zou u ons meer kunnen vertellen?

http://mathworld.wolfram.com/Helix.html
Deze is ons duidelijk
http://mathworld.wolfram.com/Helicoid.html
Deze beredenering kunnen we niet volgen

Hier staat in ieder geval wat informatie. Maar de formules
http://mathworld.wolfram.com/SphericalHelix.html dit lijkt een gecombineerde formule maar wij kunnen hier geen beeld van vormen en is dit wel van toepassing op ons 'probleem'?

Het probleem ligt een beetje in de discrete verandering en dus niet de continuë. De spoeldraad heeft namelijk een vast dikte waardoor de straal met vaste stapjes toeneemt. Dan zit je vaak met som formules.

Dit lijkt ons eerst wel even genoeg.

We hopen dat jullie ons verder op weg kunnen helpen.

Alvast bedankt
Cees W
Leerling bovenbouw havo-vwo - donderdag 29 januari 2004

Antwoord

In principe zou ik de formule van Lengte van papier gebruiken. Gebruik hierbij dan als 'dikte' van het papier de dikte van één winding. Dit laatste is steeds hetzelfde. Blijft over het aantal windingen per 'laag'.

Een voorbeeld. Ik heb een draad van 2 mm. Daarvan maak ik een spoel met d=100 mm en D=120 mm. Op een 'laag' zitten 20 windingen.

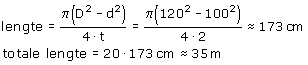
Het niet eens zo moeilijk een algemene formule af te leiden voor dit probleem (met l:lengte van de spoel), maar dat mag je dan zelf doen.

Zie ook Lengte van een rol stof.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 31 januari 2004