WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Homothetie

Ik kan geen enkele oefening goed maken. Een voorbeeld...

gegeven:(A,A') € h(O,k)
h(B)= B'
h(C)= C'

Gevraagd: Zoek B en C

Dit is het gene wat ik niet kan.

Gysens
2de graad ASO - maandag 19 januari 2004

Antwoord

Beste Jimmy,

Analyse: Onder homothetie wordt een driehoek ABC afgebeeld op een driehoek A'B'C' waarvan de zijden parallel zijn. Dus AB is parallel aan A'B', AC is parallel aan A'C' en BC is parallel aan B'C'.

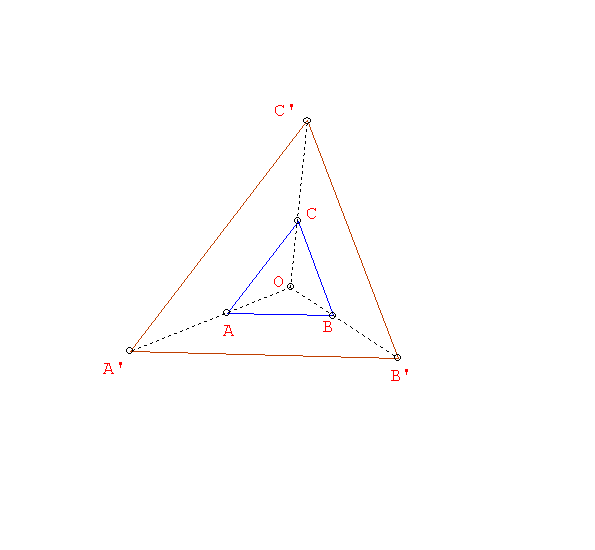
Er van uit gaande dat gegeven zijn: O, A, A', B' en C', met geen enkel tweetal punten van A'B'C' collineair met O, de volgende constructie:

Teken de lijnen OA', OB' en OC'. A ligt op OA'. Construeer de lijn l door A evenwijdig met A'B'. Het snijpunt van l en OB' geeft punt B. C vind je op soortgelijke wijze.

******

Er kan een probleem ontstaan als er wel een tweetal punten collineair zijn met O. In de volgende figuur zijn ABC gegeven en collineair met O. Ook A' is gegeven als beeld van de homothetie. Hoe nu B'en C' te vinden?

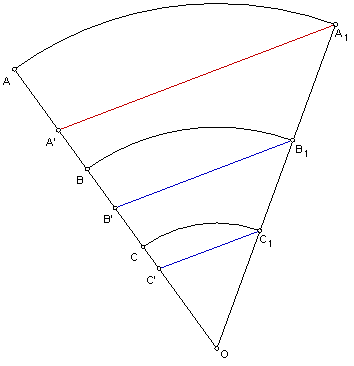
We maken een tweede lijn door O. We roteren ABC naar A₁B₁C₁. Nu trekken we de lijn A'A₁. De punten B' en C' vinden we nu door lijnen te trekken door B₁ en C₁ en te snijden met de lijn OABC.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 20 januari 2004