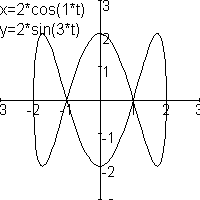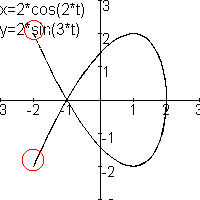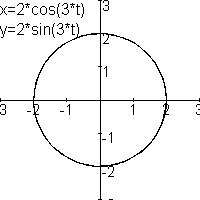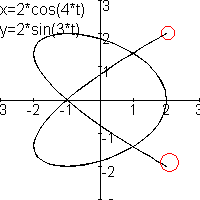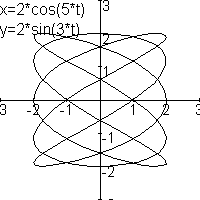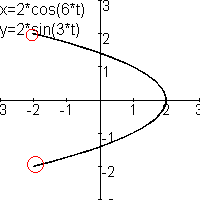WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Keerpunten bij Lissajousfiguren

Hallo, ik snap de volgende vraag niet:

Gegeven zijn de parametervoorstellingen:

x=2 cos n t
y=2 sin 3 t

het domein is [0,2p]

Neem n een geheel getal 1,2,3,....,6
Bij welke waarden van n krijg je een kromme zonder keerpunten?

Ik weet alleen dat je keerpunten hebt als je de afgeleide van x gelijk stelt aan nul en afgeleide van y gelijkstelt aan nul.

groetjes,

toktok
Leerling bovenbouw havo-vwo - zondag 18 januari 2004

Antwoord

Een keerpunt is een punt op een kromme waar de bewegingsrichting omkeert.
Het is misschien wel handig om eerst eens even de 6 verschillende krommen te plotten.
Hieronder komen ze:

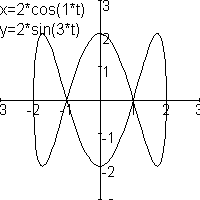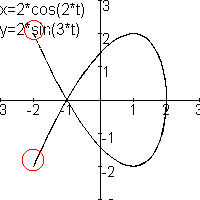
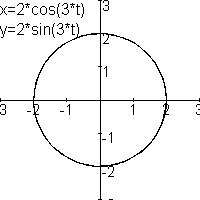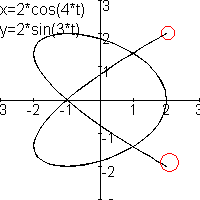
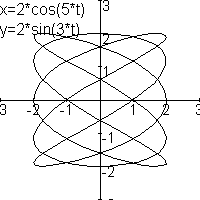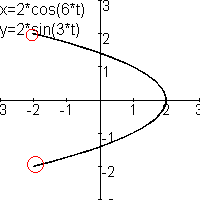
Er is een essentieel verschil tussen de plaatjes met n=1, n=3, n=5 en de plaatjes met n=2, n=4 en n=6.
De krommen met n=2,4 of 6 hebben keerpunten, deze heb ik met een rood cirkeltje aangegeven. De krommen met n=1, 3 en 5 hebben geen keerpunt. De vraag is hier dus mee beantwoord.
Nu de verklaring.
Waarom heeft de kromme met n=2 een keerpunt.
Hieronder heb ik de "gewone" grafieken van f(x)=2cos(2t) en g(x)=2sin(3t) getekend:

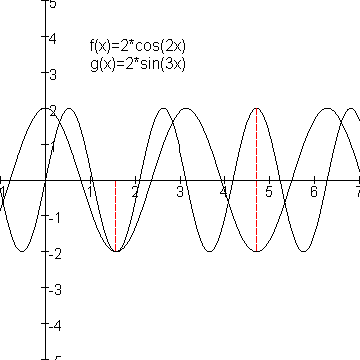
Wat je ziet is dat deze twee grafieken voor t=1/2p en t=1,5p beide een extreme waarde hebben. Wat gebeurt er nu rond t=1/2p met de bijbehorende kromme? Voor toenemende t nemen x en y eerst af en daarna weer beide toe: de bewegingsrichting keert om.
Rond t=1,5p neemt de ene eerst toe en daarna af, de andere neemt eerst af en daarna toe. Ook hier keert de bewegingsrichting om. Iets dergelijks doet zich ook voor bij n=4 en n=6.
Bekijk nu het geval met n=1:

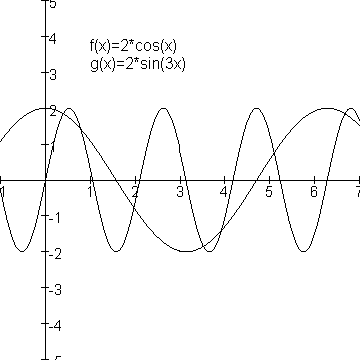
Nergens is er sprake van het gelijktijdig omkeren van de beide bewegingsrichtingen. Er is dus ook geen keerpunt.
Ook voor n=3 en n=5 lukt het niet om zulke punten te vinden.

Rekentechnisch kun je dit soort punten op het spoor komen door de afgeleiden van x en y beide nul te stellen. Mochten er waarden van t zijn waarvoor beide afgeleiden tegelijk nul worden dan zijn de bijbehorende punten van de kromme sterke kandidaten voor keerpunten.
Probeer dit maar eens netjes uit te voeren voor de zes genoemde krommen.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 19 januari 2004