|
|
|
\require{AMSmath}



Vergelijkingen en ongelijkheden van de tweede graad
Voor welke waarden van a ligt de grafiek van f(x)=3ax2+3ax+a+1
1. geheel boven de x-as?
2. geheel onder de x-as?
Dank u wel voor het beantwoorden van deze vraag.
Met vriendelijke groet,
Sébastien
Sébast
Iets anders - zondag 18 januari 2004
Antwoord
Om deze vraag te bantwoorden moet eerst een andere vraag beantwoorden:
wanneer heeft de grafiek geen snijpunten met de x-as?
Deze snijpunten vind je met de abc-formule:
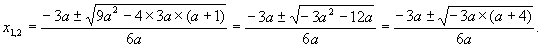
Deze snijpunten zijn niet reëel te bepalen (d.w.z. de grafiek snijdt de x-as niet) als de determinant kleiner is dan 0, oftewel als -3a(a+4)  0. Dat is het geval als x Î 0. Dat is het geval als x Î  -¥,-4 -¥,-4 È È  0,¥ 0,¥ . .
Verder moet je je realiseren dat de grafiek van een tweedegraadsfunctie een parabool is, d.w.z. dat de grafiek altijd ofwel concaaf, ofwel convex is.
(1) Als de grafiek geheel boven de x-as ligt, is zij strict convex, d.w.z. dat f''(x)  0. f''(x) = 6a (ga na!), dus de grafiek is strict convex als a 0. f''(x) = 6a (ga na!), dus de grafiek is strict convex als a  0. Dit komt overeen met het tweede deel van het domein, dus het antwoord op je eerste vraag is: als x Î 0. Dit komt overeen met het tweede deel van het domein, dus het antwoord op je eerste vraag is: als x Î  0,¥ 0,¥ . .
(2) Als de grafiek geheel onder de x-as ligt, is zij strict concaaf, d.w.z. dat f''(x)  0. De grafiek is strict concaaf als a 0. De grafiek is strict concaaf als a  0. Dit komt niet overeen met het domein, dus het antwoord op je eerste vraag is: als x Î 0. Dit komt niet overeen met het domein, dus het antwoord op je eerste vraag is: als x Î  -¥,-4 -¥,-4 . .
KLY
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 18 januari 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








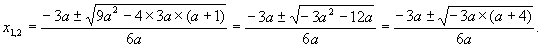
 0. Dat is het geval als x Î
0. Dat is het geval als x Î  È
È 