WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Gelijkbenige driehoek heeft gelijke basishoeken en Thales

Hallo,
Ik heb jullie al vaker een vraag gesteld, daarbij konden jullie mij goed helpen ik hoop dat dat deze keer ook lukt. Deze vraag moet ik beantwoorden met een tekening en uitleg, het gaat over Thales van Milete ik hoop dat jullie me willen helpen:
In een gelijkbenige driehoek zijn de basishoeken gelijk.
Leg de stelling uit met behulp van een plaatje. Ik kan nergens een goed plaatje vinden en de uitleg kan ik ook niet goed formuleren! Help Me!
grx Rosa
Rosa
Leerling bovenbouw havo-vwo - zondag 18 januari 2004

Antwoord

Beste Rosa,

Neem een driehoek ABC met AB=AC. Dan kunnen we een cirkel tekenen met middelpunt A door B en C. Ook kunnen we op die cirkel het punt D tekenen, zodat CD een diameter is door de cirkel (A ligt op CD).

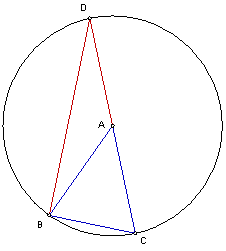
Met de Stelling van Thales weten we nu dat hoek CBD recht is.

Nu kunnen we hetzelfde weer doen door punt E te nemen op de cirkel zodat BE een diameter is van de cirkel.

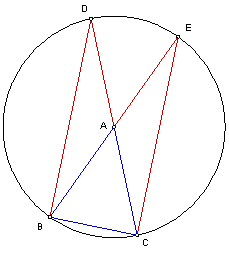
Nu zien we met de Stelling van Thales dat hoek BCE recht is.

We kunnen nu de conclusie trekken dat BCE en CBD congruente driehoeken zijn. Immers, CD en BE zijn allebei diameters in dezelfde cirkel, BC is gelijk in beide driehoeken, en de derde zijde is via de stelling van Pythagoras dus ook gelijk. De twee driehoeken hebben dus drie gelijke zijden, en moeten precies identiek zijn. Dat de overeenkomende hoeken gelijk zijn is ook de basis van de welbekende goniometrische verhoudingen sinus, cosinus en tangens!

De hoeken CBE en BCD zijn dus ook gelijk, precies dat wat we wilden aantonen.

Overigens vind ik het een heel gedoe om hiervoor de stelling van Thales uit de stal te trekken. Ik prefereer hier om gewoon de hoogtelijn uit A naar F op BC te trekken. Dan zijn AFB en AFC op eenzelfde manier als hierboven congruente driehoeken.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 18 januari 2004