WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Diagonaal van een parallellogram

Kan je me aub helpen met dit meetkundig probleem

Vierhoek ABCD is een parallellogram. Vanuit het hoekpunt B vertrek een rechte op die een punt E gemeenschappelijk heeft met het lijnstuk AD, vanuit hoekpunt D vertrekt eveneens een lijn die een punt F gemeenschappelijk heeft met het lijnstuk BC.
Vanuit hoekpunt A vertrekt een diagonaal naar hoekpunt C die het lijnstuk BE kruist in punt G en het lijnstuk FC kruist in punt H.
BE // FD
AE = 1/3 ED
FC = 1/3 BF

Te bewijzen: AC = 5 AG

Ik weet dat het ingewikkeld klint maar ik kan geen tekening maken, zou u mij aub kunnen op weg helpen?
Alvast bedankt
Sofie
Polleu
Ouder - vrijdag 16 januari 2004

Antwoord

Eerst een tekening:

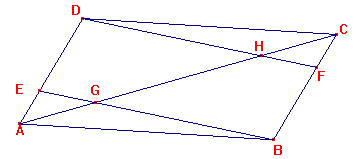
Een schets: omdat DAGE~DAHD kan je laten zien dat AG=¹/₄AH.
Ook is DAGEºDCHF (congruent). Dus AG=CH.
Zou dat zo lukken?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 17 januari 2004

Re: Diagonaal van een parallellogram