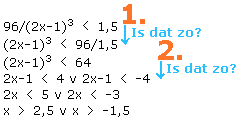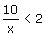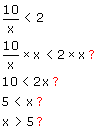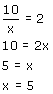WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Gebroken vergelijking en ongelijkheid

hoi ik heb een beetje een probleem met het oplossen van gebroken vergelijkingen.
bijvoorbeeld 96/(2x-1)³ 1,5
als ik het uitvoer dan krijg ik maar 1 antwoord en het 2e antwoord is dan fout.
96/(2x-1)³ 1,5
(2x-1)³ 96/1,5
(2x-1)³ 64
2x-1 4 v 2x-1 -4
2x 5 v 2x -3
x 2,5 v x -1,5

kan iemand mijn fout die ik heb begaan aub vertellen of vertellen hoe het wel moet?
vbd
Steven
Leerling bovenbouw havo-vwo - maandag 12 januari 2004

Antwoord

Er zitten in ieder geval twee fouten in die ik zal bepreken, omdat ze belangrijk zijn! En van fouten kan je leren, dus dat is dan weer mooi meegenomen...

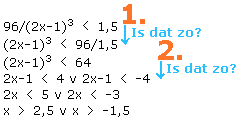
Bij 1. doe je iets vreemds! Ga maar na, neem even (voor het gemak) aan dat er dit stond:

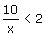
Op jouw manier zou je concluderen:

x10/2
x5

Maar is dat zo? Als ik x=2 neem dan klopt het al niet, terwijl 2 toch echt kleiner is dan 5. Ook erg:

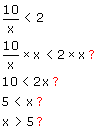
Klopt dat dan? Nee ook niet! Kan je je nog herinneren dat het teken omklapt als je vermenigvuldigt met (of deelt door) een negatief getal? Hoe weet je nu hier of 'x' niet negatief is? Dat weet je dus niet...

Hoe dan wel?
Bij 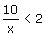reken je eerst uit waar 'ze' gelijk zijn:

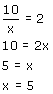
Nu is er echter nog een probleem! x mag geen nul zijn! Als de grafiek (grafiek?... komt straks) daar een asymptoot heeft, dan kan daar ook nog tekenwisseling plaats vinden! Dus ik heb nu (in feite) drie gebieden:

x:-----0---5------

Voor x0 is de ongelijkheid waar.
Voor 0x5 is de ongelijkheid niet waar.
Voor x5 is de ongelijkheid waar.

Dus het antwoord zou moeten zijn:
x0 of x5

Nog een foutje...
Bij 2. staat ook nog iets vreemds... je doet net alsof (2x-1)³ een parabool is, maar dat is niet het geval. Het is een derdegraads functie... dus geldt niet dat als (2x-1)³=64 dat 2x-1=-4. Ga maar na: (-4)³=-64.

Nee... dat schiet niet op, de rest klopt wel, maar heeft nu niet zo veel zin meer... begrijp je...

Zelf proberen...
Ik zou het (als je dat echt zo wilt doen) anders aanpakken.
Eerst gelijkstellen en los de vergelijking op.
Onderzoek of er sprake is van asymptoten... (beschouw het linker- en rechterlid als functies!).
Maak een tekenverloop en onderzoek de verschillende intervallen apart...
Kortom een heel gedoe... maar probeer het eens... mocht het niet lukken, dan reageer maar even, want er zijn vele wegen die naar Rome leiden...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 12 januari 2004