|
|
|
\require{AMSmath}



Getallenstelsel Maya`s
Hoe gaat het getallenstelsel van de maya's in zijn werk, als je kijkt naar vermenigvuldigen, delen, worteltrekken en machtsverheffen...?
Rik su
Leerling bovenbouw havo-vwo - maandag 12 januari 2004
Antwoord
Het is niet zeker of Maya's zelf konden vermenigvuldigen, laat staan delen, worteltrekken of machtsverheffen. Volgens sommigen deden ze 'een poging tot' vermenigvuldigen door gewoon herhaaldelijk op te tellen. 4X30 zou dan resulteren in 30+30+30+30. Leuk tijdverdrijf als het om grotere getallen gaat  . .
Er is wel een methode ontwikkeld (Lamberd, Ownbey-McLaughlin en McLaughlin) die ons in staat stelt te vermenigvuldigen van kleinere getallen(Het is echter zeer betwijfelbaar of die onder de Maya's bekend was). Deze methode is gebaseerd op drie eenvoudige regels:
punt X punt = punt
punt X lijn = lijn
lijn X lijn = lijn en punt op een hoger niveau
Een uitgewerkt voorbeeldje:
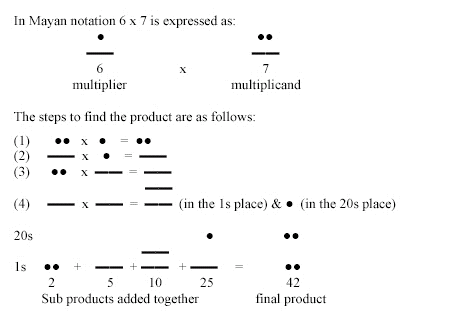
Ook voor delen en vermenigvuldigen van grotere getallen ontwikkelden ze een methode. Je kan dit allemaal uitgebreid nalezen in een verslag over de wetenschappelijke kennis van de Maya's van Arellano Angelica.
Maya's lagen wellicht niet wakker van worteltrekken of machtsverheffingen. Niettemin moet hun kennis niet onderschat worden. Ze werkten reeds met negatieve getallen en kenden reeds een voorstelling voor het getal 0 voor dit in onze gewesten algemeen bekend was.
Zie Maya Mathematics
Iris
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 13 januari 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 .
.
