WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Puzzel23

hoi,

je gaat driehoeken tekenen. de lengte van iedere zijde moet een geheel aantal cm zijn en de omtrek van de driehoek moet 15 cm zijn. Hoeveel verschillend gevormde driehoeken zijn er mogelijk?
A 1
B 5
C 7
D 19
E 45
kim
Leerling onderbouw vmbo-havo-vwo - dinsdag 6 januari 2004

Antwoord

Hoi,

De zijden zijn x, y en z. We hebben dat x+y+z=15 en dus is z=15-x-y.

De voorwaarden opdat x, y en z de zijden van een driehoek zouden vormen zijn: |x-y|zx+y, |x-z|yx+z en |y-z|xy+z. Omwille van de symmetrie zullen alle permutaties van x,y en z meervoudig geteld worden. We kunnen dus eisen dat xyz.

De voorwaarden worden dan: x-yz, zx+y, x-zy, yx+z, y-zx en xy+z.

Met z=15-x-y worden deze:
x-y15-x-y, 15-x-yx+y, x-(15-x-y)y, yx+(15-x-y), y-(15-x-y)x en xy+(15-x-y) of:
x7.5, 7.5x+y, x7.5, y7.5, y7.5 en x7.5.

Samengevat: 1zyx7 en x+y8.

In het plaatje stel ik achtereenvolgens de voorwaarden voor x en y voor...

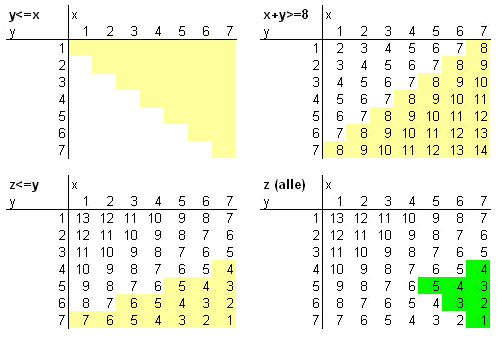
Groetjes,
Johan

andros

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 6 januari 2004

Re: Puzzel23