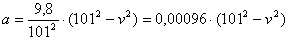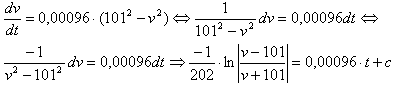WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Natuurkundige differentiaalvergelijking

Hej, de onderstaande vraag moet hoogstwaarschijnlijk met integreren en differentieren opgelost worden. Hopelijk kunnen jullie me helpen want ik kom er niet uit.

Alvast bedankt.

Gegeven:
In het luchtruim laat een motordeeltje los en valt vertikaal. Wanneer een puntmassa valt, neem de versnelling af van a = g tot nul. De verandering in versnelling kan geschreven worden als: a = (g/v²final) * (v²final-v²).

v final is de gegeven eindsnelheid.

Parameters:
v final = 101 m/s

Gevraagd:
Bepaal na hoeveel tijd (in s) de massa de gegeven eindsnelheid benaderd (99% van v final) zal bereiken wanneer men veronderstelt dat de beginsnelheid nul is.
P. van
Student universiteit - zaterdag 20 december 2003

Antwoord

Let even niet op de afrondingen, die zijn niet consequent (in significante cijfers) dat kun je zelf wat beter doen.
vfinal is gewoon een constante net als g, die eerst maar eens invullen:

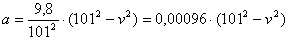
Je weet dat de afgeleide van v(t)=a(t) is dus v'=0,00096·(101²-v²)
Dit is een differentiaalvergelijking:

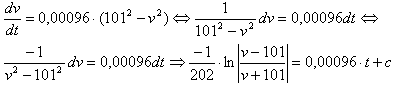
Het linkerdeel van de oplossing gaat volgens een standaardintegraal. Aangezien V(0)=0 kun je eenvoudig inzien dat in het rechterdeel van de oplossing c=0 moet zijn.
Nu wil je weten wanneer je snelheid 100m/s bereikt. Dat is vervolgens nog slechts een kwestie van invullen. Na ruim 27 seconden dus. Gevoelsmatig zou dat best eens kunnen kloppen.

Met vriendelijke groet

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 21 december 2003