WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Construeer een vierkant met dezelfde oppervlakte als een driehoek.

Gegeven een driehoek ABC met lengte AC=6 en hoogte op AC=9

Je moet het volgens twee manieren kunnen oplossen:
volgens de 2 projectiestellingen:
in een rechthoekige driehoek is het kwadraat van de hoogte op de schuine zijde gelijk aan het product van de loodrechte projecties van de rechthoekszijden op de schuine zijde
In een rechthoekige driehoek is het kwadraat van een rechthoekszijde = het product van de SZ en de loodrechte projectie van deze rechthoekszijde op de SZ.
Kunnen jullie me alstublieft helpen?

Bedankt
Kevin
2de graad ASO - maandag 15 december 2003

Antwoord

dag Kevin,

Je zult wel begrijpen dat de oppervlakte van het vierkant gelijk moet zijn aan 27.
De zijde van het vierkant is dus gelijk aan √27.
ofwel: 3√3.
De vraag is dus: hoe construeer je een zijde met zo'n lengte, en hoe gebruik je daarbij een van de projectiestellingen.
Laten we de eerste projectiestelling bekijken, misschien kun je de tweede dan zelf toepassen.
In de stelling staat dat (in een rechthoekige driehoek) het kwadraat van de hoogte gelijk is aan het product van twee projecties.
27 is het product van 3 en 9.
We kunnen nu twee lijnstukken tekenen, AS en SB (aan elkaar) met lengtes 3 en 9, en dit moeten dan de projecties worden.
In het gezamenlijke punt S trekken we dan een loodlijn: daar moet de hoogte op komen te liggen.
Nu moeten we nog zorgen dat het een rechthoekige driehoek wordt. Dat kunnen we doen, door een halve cirkel met middellijn AB te snijden met de loodlijn: snijpunt C.
Hoek ACB is dan recht.

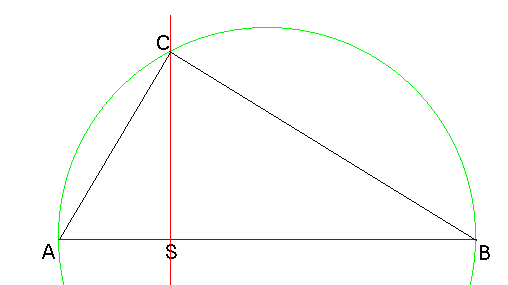
SC is dan de lengte van de gevraagde zijde van het vierkant.
Lukt het nu ook met gebruik van de tweede projectiestelling?
succes.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 16 december 2003