|
|
|
\require{AMSmath}



Toon aan...
Via een figuur hebben we dit vastgesteld. Maar hoe kunnen we dit bewijzen?
Wanneer je in een driehoek een hoogtepunt verbindt met 2 van de 3 hoekpunten , dan is het derde, overblijvende hoekpunt het hoogtepunt van de nieuwe driehoek.
Thx.
Miguel
Student universiteit - zondag 14 december 2003
Antwoord
Eigenlijk is er niet zoveel te bewijzen.
We weten dat de hoogtelijnen van een driehoek door één punt gaan.
Van driehoek ABC is het hoogtepunt het punt H.
Kijk nu eens naar onderstaande figuur.
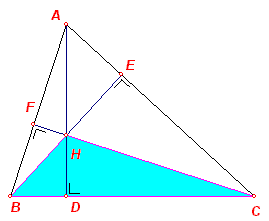
De hoogtelijnen van driehoek BCH staan loodrecht op: CH (hoogtelijn is de lijn BA), HB (hoogtelijn is de lijn CA) en BC (hoogtelijn is de lijn DA).
En eigenlijk staat het er dan al:
het punt A ligt op BA, CA, DA.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 14 december 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










