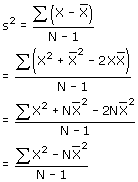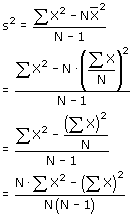WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Drie formules voor de standaaddeviatie

Hoi,
Ik heb drie formules voor de standaarddeviatie: a, b en c.

Vraag 1: Volgens het boek is formule b. afgeleid van a. Hoe kan dat, want X²-Y²¹(X-Y)²? De logica ontgaat mij.

Vraag 2: Welke van de drie formules is de meest precieze?

NB bij formules a. en b.:
Boven elke åteken staat N en eronder staat i=1.
Rechtsonder elke X staan een i.

M = gemiddelde = åXi/N (som van alle x-en gedeeld door aantal x-en)

Formule a: S = Ö(åX²/N - M²)

Formule b: S = Ö(å(X-M)²/N)

Formule c: S = Ö(åX² - (åX)²/n)/n-1

Alvast bedankt voor het meedenken. Ben hier al deze hele zondagmiddag mee aan de weer.
Shanti
Student universiteit - zondag 7 december 2003

Antwoord

Volgens mij gooi je hier een paar formules door elkaar. Voor de variantie in ieder geval twee formules die zich redelijk eenvoudig uit elkaar laten afleiden:

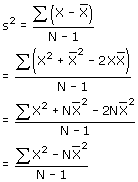
Er is nog een formule, zonder het gemiddelde:

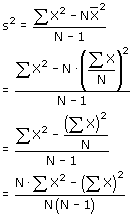
Waarmee we dus 3 formules hebben voor de variantie. De standaarddeviatie is dan natuurlijk de wortel van de variantie.

Hopelijk brengt dat wat verheldering...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 8 december 2003