WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Bol

Stel je hebt een bol en je tekent daar een cirkel op. Als ik de oppervlakte weet van die cirkel op de bol (dus een bolkap), kan ik dan ook berekenen wat de oppervlakte is van een "zeshoek" om die bolkap OP de bol? Waarbij geldt dat de "zijden" van de "zeshoek" raken aan de bolkap.

p.s. in het platte vlak is het natuurlijk eenvoudig, maar is dat nou hetzelfde op een bol, ik denk het niet, vandaar deze vraag

Bij voorbaat dank voor uw hulp.
Arjun
Leerling bovenbouw havo-vwo - zondag 7 december 2003

Antwoord

Hoi,

Je hebt een bol met straal R en een cirkel op die bol met straal r (die je eventueel berekent uit de gekende oppervlakte van die cirkel).
Je hebt verder een regelmatige 6-hoek op die cirkel die dus zijde r zal hebben.
Je hebt het ook over een 6-hoek 'op' de bol. Nauwkeuriger geformuleerd gaat het om een symmetrisch prisma met als grondvlak de 6-hoek en een top op de bol. Bemerk dat er in het algemeen 2 van die prisma's zijn: ééntje met de top boven en een ander met de tophoek onder het vlak van de cirkel. Je kan de oppervlakte van de opstaande driehoekjes van dit prisma berekenen als je de lengte x van een opstaande ribbe kent.
We snijden het prisma met een vlak loodrecht op dat van de cirkel, door de tophoek en door 2 overstaande zijden.

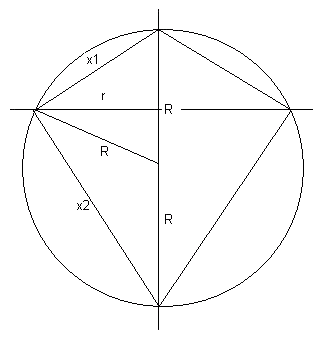
We zien een rechthoekige driehoek met zijden x₁, x₂ en 2R en hoogte r. Volgende betrekkingen gelden:
x₁.x₂/2=2R.r/2 (oppervlakte uitdrukken)
x₁²+x₂²=(2R)² (Pythagoras)

Hiermee vind je dan x₁ en x₂, de 2 mogelijke waarden voor de opstaande ribben. Met de formule van Heroon kan je de oppervlakte van een driehoek berekenen in functie van de zijden.

Groetjes,
Johan

andros

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 9 december 2003

Bol(2)