WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Veranderen van referentiestelsel met hoeken

mijn probleem is dat ik in de cursus programmeren een klok moet implementeren, hierbij moet ik dus mijn assenstelsel draaien en omkeren.
ik heb het ooit al gedaan, maar ik zou niet meer weten hoe.
dus nu is( in het oude assenstelsel) :
0h = 90° = p /2 rad
1 h = 60° = p /3 rad
...
3h = 0° = 0 rad
...
10h = 300° = 5 p / 6

en dat moet worden ( nieuwe assenstelsel )
x h = x * ( p / 6 )

bedankt
Dehaes
Student universiteit - donderdag 4 december 2003

Antwoord

Ik zie twee manieren waarop je dit zou kunnen oplossen.
Bij de eerste manier hou je de notatie van de eenheidscirkel, maar zorg je dat je hoek op een andere manier afhankelijk is van de tijd.
Bij de tweede manier kies je de hoek op een andere manier dan in de eenheidsdriehoek.

Ik ga er even vanuit dat je alleen moeite hebt met de hoek, en dat het bepalen van de coördinaten van het einde van de wijzer als je de hoeken weet geen probleem meer is.

Methode 1
Kijk eens naar de onderstaande tekening:

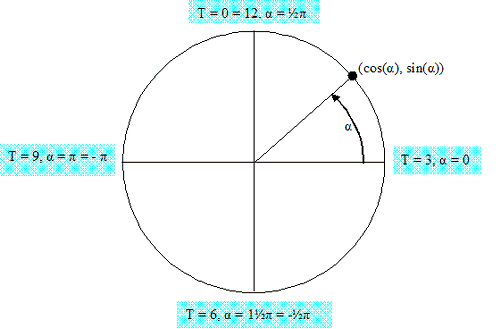
Je ziet dat je de gewone notatie als in de eenheidscirkel kunt gebruiken, maar je moet ervoor zorgen dat de tijden corresponderen met de goede hoeken.
Daarbij moet je in de gaten houden dat omdat we met een klok te maken hebben, we modulo mogen rekenen. De hoek gaat modulo 2p, de tijd T modulo 12 als je in uren rekent en modulo 60 als je in minuten rekent.
Dus:
T = 0 º 12 correspondeert met α = ¹/₂p
T = 3 correspondeert met α = 0 º 2p
T = 6 correspondeert met α = 1¹/₂p º -¹/₂p
T = 9 correspondeert met α = p º -p

Laat je T evenredig oplopen dan zou je dus a kunnen definiëren als: a = ¹/₂p – (p/6)T

Methode 2
Nu kies je de hoek op een voor een klok meer handige manier.

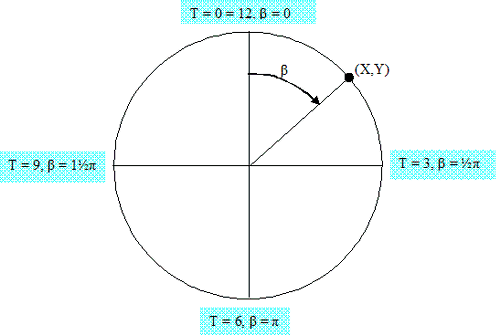
Je moet nu bepalen wat de waarde van X en Y zijn.
X = sin b
Y = cos b

Een goede oefening is om van de notatie van methode 1 naar de notatie van methode 2 te gaan met behulp van de bekende gonio formules.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 9 december 2003