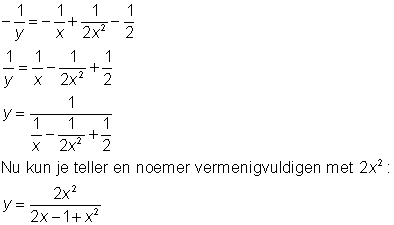WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Differentiaal vergelijkingen

Geachte heer/mevrouw,

Met de volgende som zit ik vast. Kunt u me vertellen hoe ik verder te werk moet gaan? Helaas heb ik van de opgave geen antwoord. Dus ik weet niet wat eruit moet komen.

x^3y' = xy^2 - y^2 met x=1 en y=1

y'= (xy^2 - y^2)/ x^3

dy/dx = (( x-1)y^2)/x^3
dy/y^2 = 1/x^2 dx - 1/x^3 dx

Hierin is F integraal teken

F 1/y^2 dy = F 1/x^2 dx - 1/x^3 dx

-y^-1 +c = -x^-1 +c - 1/2 x^-2 +c

Als ik dan c bereken dan krijg ik voor c=1/2 uit.

Hoe bereken ik verder y?

Met vriendelijke groet,

Bianca
Bianca
Student hbo - woensdag 3 december 2003

Antwoord

Je doet het bijna perfect.
Je maakt twee foutjes: je vergeet een minteken, en je gebruikt drie keer dezelfde letter c als integratieconstante.
Je laatste regel zou eigenlijk moeten luiden:
-y^-1 + c1 = -x^-1 + c2 + ¹/₂·x^-2 + c3 (let op de + voor de ¹/₂)
Alle constanten c1, c2 en c3 op een hoop vegen:
-y^-1 = -x^-1 + ¹/₂·x^-2 + c
waarbij c = -c1 + c2 + c3.
In dit geval maakt het toevallig niks uit als je drie keer dezelfde c neemt, maar in het algemeen kun je op problemen stuiten.
Goed dan, je hebt c correct berekend met de foute formule. Bij de goede formule krijg je c = -¹/₂
Je krijgt dus:

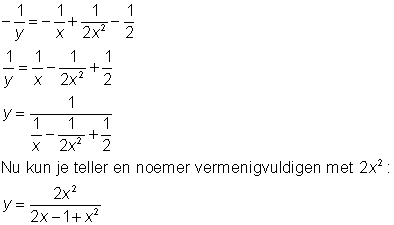
Overigens kun je er ook voor kiezen om de c pas op het laatst berekenen.
groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 3 december 2003