WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Voorwaardelijke kansen en onafhankelijkheid

Op dit moment ben ik bezig met kansrekenen en kom ik op de volgende rare opgave:

Als geldt P(A|B) = 0,30 en P(A en B) = 0,20 dan is P(B) gelijk aan:

0,06
0,50
0,667
0,60

Kunt u mij helpen met het oplossen van de vraag, ik heb geprobeerd het 1 en ander op te lossen d.m.v tutorials, maar ik kan hier niks over vinden, hoe dit op te lossen.

Hetzelfde heb ik met deze opgave:

Als geldt dat P(A) = 0,30 en P(B) = 0,70 en tevens dat de gebeurtenissen A en B onderling onafhankelijk zijn, dan geldt P(A en B) = ...
0,21
0,40
1
0,4286

Felix
Student hbo - maandag 1 december 2003

Antwoord

Dit soort 'problemen' kan je handig oplossen met behulp van een kanstabel:

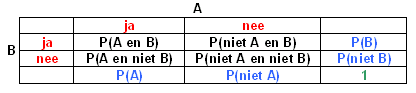
P(A|B) is de kans op A als B! Uit bovenstaande tabel kan je dat vinden met:

$
\eqalign{P\left( {A|B} \right) = \frac{{P\left( {A\,\,en\,\,B} \right)}}
{{P\left( B \right)}}}
$

Zie 4. Voorwaardelijke kans.

Bij de eerste vraag een kwestie van invullen!

0,30=0,20/P(B)
P(B)0,667

Als de gebeurtenissen A en B onafhankelijk zijn dan geldt:

P(A en B)=P(A)·P(B)

Zie 5. (On)afhankelijkheid.

In dit geval wederom een kwestie van invullen.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 1 december 2003