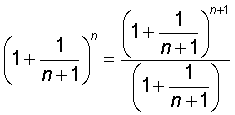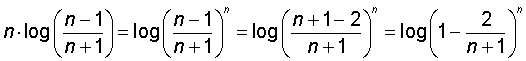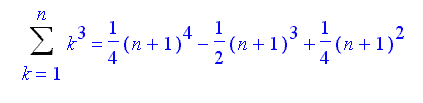WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hoe bereken ik de volgende limieten?

Hallo ik heb een paar vraagjes:
Hoe bereken ik de volgende limieten?

lim n®¥ de n-de machtswortel uit n²+7n+31

lim n®¥ (1+ (1/n+1))tot de n-de

lim n®¥ n log (n-1/n+1)

lim n®¥ de n-de machtswortel uit 1³+2³+3³+4³+...+n³

Ik zou graag willen weten hoe ik dit aan moet pakken.
Teddy
Student hbo - dinsdag 25 november 2003

Antwoord

dag Teddy,

Om te beginnen met de eerste:
Weet je dat je de n-de machtswortel uit a kunt schrijven als a tot de macht ¹/_n?
Dan ligt het voor de hand om de logaritme te nemen.
Vervolgens krijg je een breuk, waarvan je de limiet kunt berekenen met de stelling van de 'l Hôpital.
Lukt dat dan?
Dan de tweede:
Die lijkt wel erg sterk op de standaardlimiet waar het getal e uitkomt.

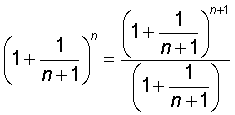
Brengt dit je op een idee?
De derde: ik denk dat het volgende jouw bedoeling is:

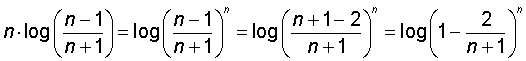
en dat moet je ook bekend voorkomen.
De laatste limiet veronderstelt naar ik aanneem, dat je bekend bent met de formule:

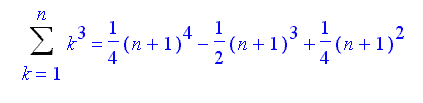
Zie verder de tip bij de eerste limiet.
Hopelijk ben je zo op weg geholpen.
succes.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 25 november 2003