WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Poolvergelijking

Kan u mij helpen deze vraag op te lossen?

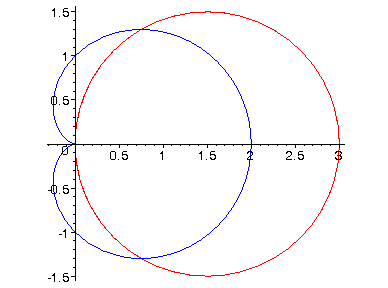
onder welke hoek snijden de krommen r= 3cos(q) en r= 1+ cos(q) elkaar?

bedankt
jos

jos
Student Hoger Onderwijs België - donderdag 20 november 2003

Antwoord

We gaan proberen om dy/dx van beide krommen in het snijpunt te berekenen. In wat volgt stel ik voor het gemak van de invoer q voor door t en r door r.

x = r(t) cos t
y = r(t) sin t

dx/dt = r'(t) cos(t) - r(t) sin(t)
dy/dt = r'(t) sin(t) + r(t) cos(t)

dy/dx
= (dy/dt)/(dx/dt)
= (r'(t) sin(t) + r(t) cos(t)) / (r'(t) cos(t) - r(t) sin(t))
= (r'(t) tan(t) + r(t)) / (r'(t) - r(t) tan(t))

De hoek die de raaklijn maakt met de x as is gegeven door arctan(dy/dx). Zoek de waarde van t waarvoor het snijpunt in kwestie optreedt, bepaal voor beide krommen de hoeken die de bewuste raaklijnen maken met de x-as en trek die van elkaar af. Lukt het zo?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 21 november 2003