WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

De som van de hoeken in een driehoek

In welke stap van het volgende bewijs maak je gebruik van de stelling dat de hoekensom in een driehoek 180 graden is?

Gegeven
AP en BQ zijn lijnen die aan dezelfde kant van AB liggen zodat hoek BAP + hoek ABQ = p–g met g0.

Te bewijzen
BQ snijdt AP (het paralellenpostulaat).

Bewijs
De hulpstelling zegt dat we een punt C op AP kunnen vinden zodat hoek ACB is kleiner is dan g.
Dan geldt (3) hoek BAP + hoek ABC = p – hoek BCA is groter dan p–g. En dus volgt dat hoek ABC is groter dan hoek ABQ. Punt Q ligt dus in het binnengebied van driehoek ABC en de lijn BQ moet daarom AC snijden.

chris
Leerling bovenbouw havo-vwo - maandag 17 november 2003

Antwoord

Hoi,

Volgend plaatje maakt één en ander duidelijk. Ik definieer er de hoeken a, b en g en alle andere symbolen uit het vervolg van mijn uitleg mee.

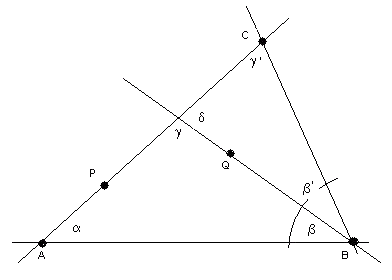
Uit je hulpstelling heb je dat er een punt C bestaat (aan dezelfde kant van AB als P) zodat: g'g (met g' zoals op het plaatje) en dus: p-g'p-g

Omdat de som van de hoeken in DABC precies p is, hebben we: a+b'+g'=p, zodat p-g'=a+b'. Verder is ook gegeven dat p-g=a+b.

Onze ongelijkheid wordt dus: a+b'a+b of bb'. Omdat Q ook aan dezelfde kant van AB ligt als P, volgt inderdaad dat de halfrechte BQ in de vlakhoek ABC moet liggen (niet dat Q binnen DABC ligt - Q kon evengoed op BQ liggen, maar aan de andere kant van AP). Daarom moet BQ snijden met AP in een punt tussen A en C.

Merk op dat je deze stelling misschien makkelijker uit het ongerijmde kon bewijzen. Als AP // BQ, dan is a+b=p, zodat g=0. Omdat we weten dat g0 is de veronderstelling fout en moeten AP en BQ dus snijden.

Groetjes,
Johan

andros

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 20 november 2003