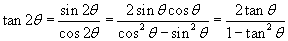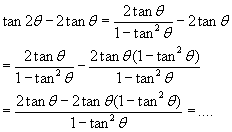WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

2 eenvoudige vragen

Ik zit met 2 eenvoudige vragen. Ik weet alleen niet hoe eraan de beginnen .

Bewijs dat :

cos⁶ x - sin⁶ x = cos2x - ¹/₄ cos2x.sin²2x

en

tg²0. tg 20 = tg 20 - 2 tg 0

Alvast dank om mij "op gang" te helpen

rogeke
rogeke
3de graad ASO - zaterdag 15 november 2003

Antwoord

1.

Deze kun je het beste beginnen met het rechterlid, en dan bewijzen dat deze uiteindelijk gelijk is aan het linkerlid.

cos2x - ¹/₄cos2x.sin²2x
= cos²x-sin²x - ¹/₄.(cos²x-sin²x).4sin²x.cos²x
= cos²x-sin²x - sin²x.cos⁴x + sin⁴x.cos²x
= cos²x(1+sin⁴x) - sin²x(1+cos⁴x)
= (1-sin²x)(1+sin⁴x) - (1-cos²x)(1+cos⁴x)
= 1 + sin⁴x - sin²x - sin⁶x - 1 - cos⁴x + cos²x + cos⁶x
= cos⁶x - sin⁶x + sin⁴x - sin²x - cos⁴x + cos²x
= cos⁶x - sin⁶x + sin²x(sin²x - 1) - cos²x(cos²x - 1)
... enz. probeer het laatste stapje nou eens zelf.

2.

Met die tangens heb je het telkens over 0 en 20. maar dan zou de stelling nooit kloppen. Daarom ga ik ervanuit dat je met die 0 een q bedoelt.

stap 1 welke je hiervoor moet weten is:

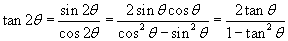
Ten tweede gaan we ook hier weer beginnen met het rechterlid, en deze uitwerken totdat we op de uitdrukking in het linkerlid uitkomen.

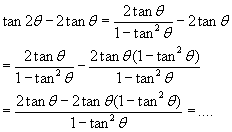
ook hier wordt je weer uitgenodigd om de laatste stap zelf verder uit te werken.

hopelijk kom je er zo verder zelf uit.

groeten,
martijn

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 15 november 2003