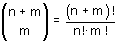|
|
|
\require{AMSmath}



Twee politieagenten patrouilleren in een stadswijk
Twee politieagenten moeten elke nacht samen in een stadswijk patrouilleren van a naar b. In mijn opgavenboek staat er een vierkant getekend met 16 hokjes en links bovenaan staat er een a en rechts onderaan een b.
De wijk bestaat uit 10 straten zoals op de figuur in mijn boek is aangegeven. De eerste agent houdt van afwisseling en wil elke nacht een andere weg volgen. De tweede agent wil in geen geval op een kruispunt een weg nemen die hem weer dichter bij a brengt.
Hoeveel nachten kunnen ze samen patrouilleren zonder in herhaling te vervallen?
Kim
3de graad ASO - woensdag 12 november 2003
Antwoord
Hoi,
Je hebt dus een stratenplan zoals in het plaatje. We veronderstellen dat het noorden naar boven is.
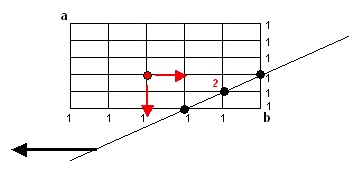
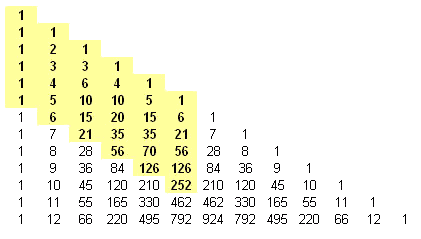
Aangezien de tweede agent steeds verder van a wil, moeten ze op elk kruispunt ofwel naar het zuiden ofwel naar het oosten. Het aantal vervolgpaden vanaf dit punt vinden we als de som van het aantal paden door het oostelijke buurpunt en die door het zuidelijke buurpunt. Vanuit alle kruispunten langs de meest zuidelijke en de meest oostelijke straat is er maar 1 pad naar b zonder dichter bij a te komen, namelijk de rechtstreekse verbinding.
Beginnend in b en opschuivend naar het westen, kunnen we achtereenvolgens voor elk kruispunt langs een diagonaal van zuid-west naar noord-oost het aantal vervolgpaden berekenen. We schrijven dit getal op het rooster zelf (zoals ik deed met 2=1+1). Op die manier komen we uiteindelijk in a. Je herkent makkelijk de getallen van de driehoek van Pascal. Het aantal verschillende paden vanuit a is dus 252.
Als je in het algemeen nxm straten hebt in een rechthoekig patroon, dan zijn er 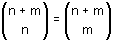 (*) verschillende paden. Je kan dit afleiden door bovenstaande redenering te veralgemenen. Je kan ook bedenken dat je een pad kan voorstellen als een rij van n keer O en m keer Z. O betekent dat we de richting oost kiezen, Z richting zuid. In totaal zijn er n+m kruispunten, het aantal paden is dus (*) verschillende paden. Je kan dit afleiden door bovenstaande redenering te veralgemenen. Je kan ook bedenken dat je een pad kan voorstellen als een rij van n keer O en m keer Z. O betekent dat we de richting oost kiezen, Z richting zuid. In totaal zijn er n+m kruispunten, het aantal paden is dus 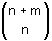 . .
Groetjes,
Johan
(*): 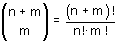
andros
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 12 november 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|









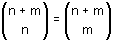 (*) verschillende paden. Je kan dit afleiden door bovenstaande redenering te veralgemenen. Je kan ook bedenken dat je een pad kan voorstellen als een rij van n keer O en m keer Z. O betekent dat we de richting oost kiezen, Z richting zuid. In totaal zijn er n+m kruispunten, het aantal paden is dus
(*) verschillende paden. Je kan dit afleiden door bovenstaande redenering te veralgemenen. Je kan ook bedenken dat je een pad kan voorstellen als een rij van n keer O en m keer Z. O betekent dat we de richting oost kiezen, Z richting zuid. In totaal zijn er n+m kruispunten, het aantal paden is dus 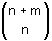 .
.