|
|
|
\require{AMSmath}



Groeifuncties
Hallo,
Ik heb enkele vraagstukken waarvan ik de opl wel weet, maar ik weet niet goed de formule ofzo.. Kunt u eens kijken?
1. Een auto verliest per jaar 18 % van zijn waarde.
- Hoeveel % van de oorspronkelijke waarde blijft er na 2,3,6,10 jaar ?
-Wat zal de waarde zijn van een auto in 1999, als de waarde in 1993 500000 BEF bedraagt?
2. Een bacteriëncultuur groeit elk uur aan met 6%.
- met hoeveel % groeit deze cultuur aan in 2uur?
- in een half uur?
- in 1/n uur?
3. Iemand wil een lening afsluiten op 20 jaar tegen 12% en wil 200 000 BEF per jaar betalen.
- Na één jaar doet hij zijn eerste afbetaling van 200 000 BEF. Wat is de waarde van deze afbetaling bij het einde van de lening ( 19 jaar later dus)
- Na twee jaar doet hij de tweede. Wat is de waarde bij het eind?
- Elk jaar volgt er een nieuwe afbetaling, de laatste na 20 jaar. Wat is de totale waarde van alle gestorte gelden bij het einde van de lening?
- De lening die wordt toegestaan (na 20 jaar) heeft dezelfde eindwaarde. Hoeveel kan er geleend worden ?
Bedankt !
a.
3de graad ASO - woensdag 12 november 2003
Antwoord
Beste Alicia,
Ik heb naar je opdrachten gekeken en ik denk dat je met de volgende formule aardig uit de voetenkan.
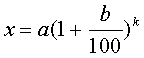
In de formule zijn: x je antwoord, a het begingetal, b het percentage, en k is de tijd (bijvoorbeeld in jaren).
Ik zal je 2 voorbeelden geven voor het gebruik van de formule.
1) Als je een bankrekening hebt, waarop je €130,- stort en je krijgt per jaar 2,5% rente, dan heb je na 2 jaar:
130(1+2,5/100)2 €136,6 €136,6
2) Als je in 1999 een auto hebt gekocht die per jaar 15% minder waard word, is je auto in 2003 nog
100(1+ -15/100)4 52,2% waard. 52,2% waard.
Let op!
Als je er een bedrag of percentage bij krijgt vul je bij b een positief getal in. Als er een bedrag of percentage af gaat vul je daar een negatief getal in.
Veel succes!
BdB
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 12 november 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








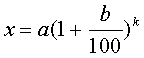
 €136,6
€136,6 