WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

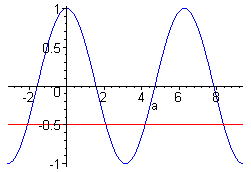
Radialen

Als je deze vergelijking moet oplossen. Hoe doe je dat dan:
los de volgende vergelijking op. Kies a uit het interval 0 tot 2 p.
cosa=-0,5
Ik hoop dat u mij kunt helpen.

ikke
Leerling bovenbouw havo-vwo - zaterdag 8 november 2003

Antwoord

Je zoekt naar een hoek a waarvan de cosinus gelijk is aan –0,5. Schrijf nu het rechterlid (-0,5) ook als een cosinus. Handig hierbij is de grafiek van de cosinus. Hieronder is afgebeeld de grafiek van y=cos(a) voor aÎ[-p,3p] en de lijn y=-0,5. De a-waarden van de snijpunten van y=cos(a) met y=-0,5 zijn de hoeken die je zoekt.

Uit de grafiek blijkt: cos(-²/₃p)=-0.5, cos(²/₃p)=-0.5, cos(⁴/₃p)=-0.5, cos(2²/₃p)=-0.5, enz.
Omdat de grafiek van y=cos(a) 'oneindig' doorgaat, is het aantal oplossingen ook eindeloos.
In het algemeen geldt: cos(A)=cos(B)ÛA=B+2pkÚA=-B+2pk met k=[0,1,2,...].
In jouw geval is aÎ[0,2p] en los je de vergelijking als volgt op:
cos(a)=-0,5Ûcos(a)=cos(²/₃p)Ûa=²/₃p+2pk Ú a=-²/₃p+2pk.
Omdat aÎ[0,2p] krijg je voor k=0® a=²/₃p+2p·0=²/₃p en voor k=1® a=-²/₃p+2p·1=⁴/₃p. De andere oplossingen (voor hogere waarden van k) vallen buiten het bereik van [0,2p].

Sander

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 9 november 2003