WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Magische vierkant van 6 x 6

ik heb veel moeite met een magisch vierkant van 6 x 6 en daardoor wil ik graag een verdere uitleg, graag wat uitgebreid.
casper
Leerling bovenbouw havo-vwo - donderdag 6 november 2003

Antwoord

Voordat je een magisch vierkant van 6x6 gaat oplossen moet je eerst en vierkant van 4x4 oplossen. Dit doen we door eerst alle getallen (1t/m16) in te vullen van boven naar beneden en vervolgens de diagonalen te draaien zo dat je het volgende krijgt.

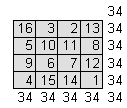
Het vierkant van 4x4 is nu correct ingevuld. Dan is het de bedoeling om bij alle zijden de uitkomst 0 te krijgen, dit kan je voor elkaar krijgen door van alle getallen 8,5 af te trekken. Nu hebben we de getallen –7,5 tot en met 7,5 in het vierkant staan, en de som is overal gelijk aan 0.

Maak nu een vierkant van 6x6 en voeg daarin (in het midden) het vierkant van 4x4 met de uitkomst 0. Nu heb je een vierkant van 36 hokjes waarvan er al 16 zijn ingevuld. We gaan nu het zelfde doen met dit vierkant, als met het vierkant van 4x4. De som moet na het invullen overal gelijk zijn aan 0.

Dit kan je realiseren door de getallen die je moet invullen zowel positief als negatief toe te voegen. In dit voorbeeld neem ik de getallen -17,5 t/m -8,5 en 8,5 t/m 17,5. Nu is het een beetje puzzelen om de getallen op de juiste plaats te krijgen. Vul eest –17,5 in op de onderste rij en daarna de 17,5 op de bovenste rij tegenover de –17,5. Op die manier zorg je ervoor dat de som van de rij van beneden naar boven gelijk blijft aan 0.

Maak nu de hele onderste rij (van links naar rechts) zo dat ook daar de uitkomst 0 van is. Na het invullen van de tegenovergestelde getallen aan de bovenkant kan je hetzelfde doen met de linker en de rechter kant. Als je het vierkant op die manier hebt ingevuld is de som overal 0. Om een vierkant te maken van 6x6 dat alleen maar positieve getallen bevat tel je overal 18,5 bij op en je vierkant is klaar.

Succes en klik vooral ook ff op de volgende link!
Zie Magische vierkanten maken

BdB

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 6 november 2003