WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Disjunct en afhankelijk

De volgende bewering moet ik bewijzen:

Als twee gebeurtenissen een strikt positieve kans hebben en disjunct zijn, zijn ze afhankelijk.

Maar ik vind hem niet logisch, want als A en B disjunct zijn geldt: P(AÇB) = 0. De kettingregel zegt P(AÇB) = P(A)P(B|A). Dat zou betekenen dat op P(A) = 0 of P(B|A) = 0. Maar wat heeft dat met afhankelijkheid te maken?

En wat wordt er bedoeld met strikt positieve kans, is een kans niet altijd positief?

Kunt u me vertellen waarom het logisch zou moeten zijn en in welke richting ik mijn bewijs moet zoeken?
Gertja
Student universiteit - zondag 2 november 2003

Antwoord

Strikt positief betekent hier dat de kans niet nul is, want zoals je al opmerkt een kans is toch altijd positief... ja.. of nul!

Laten we maar eens naar een voorbeeld kijken:

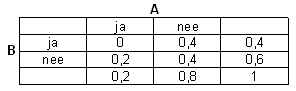
Er geldt: 'Twee gebeurtenissen heten onafhankelijk, als P(AÇB)=P(A)·P(B)'

Klopt dat hier? Nee, want P(AÇB)=0 (disjunct), dus A en B zijn afhankelijk. Dat 'ding' dat je 'kettingregel' noemt is volgens mij de definitie van 'A tegelijkertijd B' en dat klopt hier wel:
P(A)=0,2
P(B|A)=0
P(AÇB)=0

Samengevat: Als P(A)$\ne$0 en P(B)$\ne$0, maar P(AÇB)=0, dan zijn A en B afhankelijk.

..en dat is natuurlijk ook heel logisch! Onafhankelijk betekent dat de kans op A niet afhangt of de gebeurtenis B heeft plaats gevonden. Als A en B disjunct zijn dan kan A helemaal niet meer plaats vinden als B gebeurt!

Zie Voorwaardelijke kans

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 2 november 2003