WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Meetkundige plaats van een hond

Een hond bevindt zich op t=0 in het middelpunt O van een cirkel met straal 100. Zijn baas bevindt zich op dat moment in (100, 0). De baas loopt tegen de wijzers van de klok in met een constante (baan)snelheid van 1 m/s. De hond loopt vanuit het middelpunt met dezelfde baansnelheid en steeds richting zijn baas.

Vraag: Construeer de baan van de hond.

Is er iemand die over dit probleem heeft nagedacht? Ik zou graag willen weten wat je erover hebt bedacht. Ik wil dit graag in CABRI construeren, maar tot nog toe is het niet helemaal gelukt. Ik dacht: Kom, laat ik het eens met iemand delen!
Mark B
Docent - zaterdag 1 november 2003

Antwoord

Figuur 1:

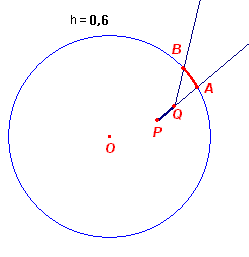
Bij dit type krommen, bekend onder de naam achtervolgingskromme (Eng. pursuit curve; Dui. Hondskurve) komt het er op neer, dat de hond probeert in een rechte lijn naar de man te rennen en daarbij dezelfde afstand aflegt als de man op de cirkel.
Die rechte lijn zal dan raaklijn zijn aan de kromme waarover de hond loopt.
In figuur 1 is een en ander geillustreerd.
Daar geldt dan (voor kleine h; voor h nadert tot 0):
bg(AB) = PQ = h
waarbij P, A en Q, B posities zijn van opvolgend de hond en de man op hetzelfde tijdstip (opvolgend t=t1 en t=t2).
Met Cabri kunnen we uitgaande van de punten P en A op de cirkel en de waarde van h de nieuwe posities (Q en B) met een macro construeren.

Figuur 2:

In figuur 2 is dat 22 keer gedaan.
Daarin is ook duidelijk te zien, dat de rechte lijnen de achtervolgingskromme - zoals dat heet - omhullen.
Figuur 2 is een Cabri-applet. De punten P, A en O (Dit punt) kunnen worden verplaatst.
Ook de grootte van de cirkel (Deze cirkel) kan worden gewijzigd.

Zie MathWorld - Pursuit Curve

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 3 november 2003