WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Taps toelopende vuurtoren

Je wilt een zeshoekige vuurtoren tekenen, die taps toe loopt. Hoe bereken je dit? Een zijde is 7 centimeter en loopt taps toe tot 6 centimeter. De vuurtoren is 30 centimeter hoog. Graag wil ik in het klein een vuurtoren maken, waarvan de onderkant een zeshoek is van zeven centimeter en loopt taps toe naar een zeskant van zes centimeter met een hoogte van 30 centimeter.

Hoe teken je nu het uitgeklapte model?
Wies O
Docent - donderdag 30 oktober 2003

Antwoord

Het grondvalk en bovenvlak
Laten we eens beginnen met de zeshoekige vlakken.

Een zeshoek is bijzonder omdat je een zeshoek kunt verdelen in 6 gelijkzijdige driehoeken.

Je kunt zo'n zeshoek daarom construeren met een passer.
Wellicht weet je hoe dat werkt, maar voor de volledigheid toch hier de constructie:

Voor het ondervlak teken je een cirkel met een straal van 7 centimeter.
Daarna laat je de afstand tussen de benen van de passer 7 centimeter.
Zet de punt op de cirkelrand en teken de snijpunten met de cirkel. Zet dan de passerpunt op zo'n snijpunt en ga zo de cirkel rond. Je hebt dan de hoekpunten van de zeshoek gevonden.

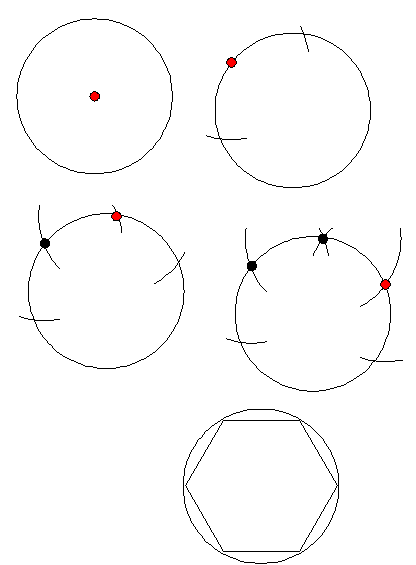
De zijvlakken
Dan de zijvlakken. Ze zullen in de vorm zijn van een trapezium. De onderzijde is 7 cm en de bovenzijde is 6 cm, maar hoe lang zijn de twee andere zijden.
Daarvoor moeten we de stelling van Pythagoras gebruiken.

Bekijk eerst een bovenaanzicht. In het rood zijn de randen van een zijvlak aangegeven.
Dan bekijken we een zijaanzicht. De blauwe gestippelde lijn geeft aan hoe.

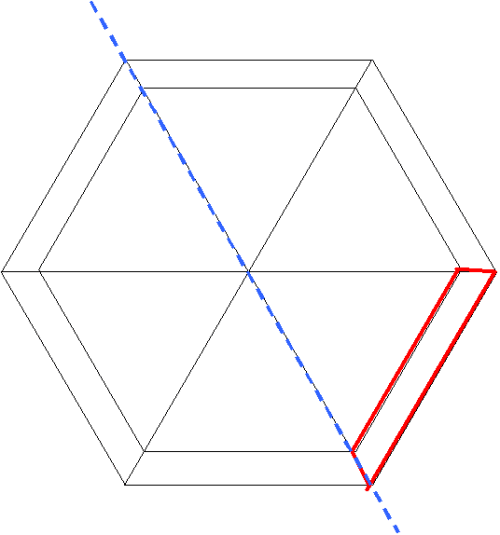
We zien nu de zijden van het zijvlak die we zoeken. We weten dat de hoogte van de vuurtoren 30 cm is en bovendien weten we dat de afstand tussen twee overstaande punten van de zeshoeken twee keer de zijde van dat zeshoek is.
De zijde die we zoeken is dus de schuine zijde van een rechthoekige driehoek met zijden 1 cm en 30 cm.
Met de stelling van Pythagoras kun je de lengte van deze driehoek berekenen. Je kunt de driehoek ook op ware grootte tekenen en dan de lengte van de schuine zijde overnemen met de passer.

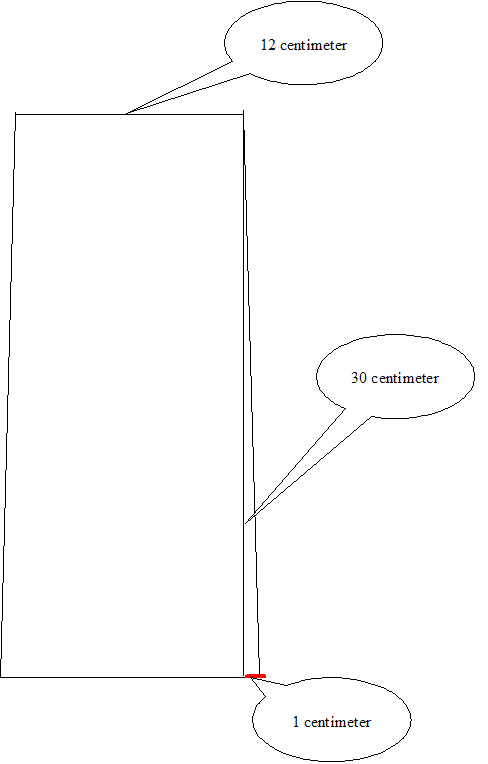
Om de zijvlakken te tekenen kan nu worden gekozen om met de stelling van Pythagoras de exacte "hoogte" van het zijvlak uit te rekenen en dat te gebruiken om de zijvlakken te tekenen.
Wil je alleen gebruik maken van passer en lineaal, dan zou je ook de basis kunnen tekenen van 7 cm, 1 cm naar binnen een loodrechte lijn trekken en met de passer de lengte van de zijde afzetten.

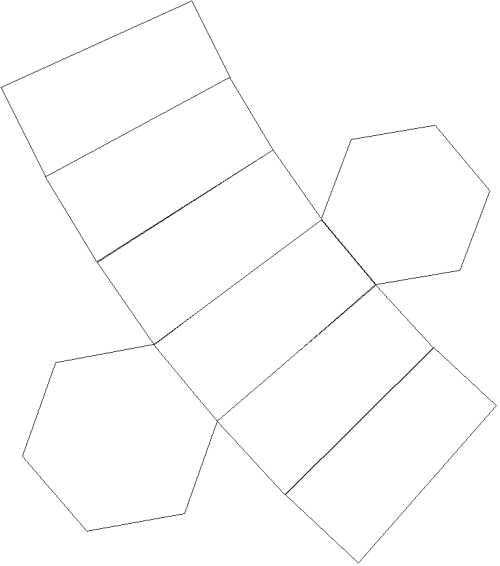
De uitslag
De uitslag zal er ongeveer als volgt uitzien. Let op, de verhoudingen kloppen hier niet. Deze uitslag zou een te lage vuurtoren geven.
De plakranden kunnen naar eigen inzicht worden toegevoegd.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 31 oktober 2003