WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

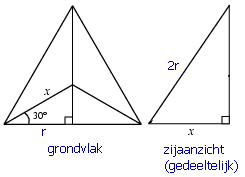
Hoogte tetraeder

Mijn opdracht is:
Ga na dat de hoogte van een tetraeder met zijden ter lengte van 2r wordt gegeven door h = ²/₃·r·√6
Gebruik hierbij dat de top van een tetraeder precies boven het midden van de onderste gelijkzijdige driehoek ligt.
Verder dan dit kom ik niet, aangezien ik in die gelijkzijdige driehoek al vastloop. Er zal wel iets met pythagoras aan de hand zijn.
Alvast bedankt.
Jonata
Leerling bovenbouw havo-vwo - donderdag 16 oktober 2003

Antwoord

Begin eens met een goede tekening (zie hiernaast).

Het zinnetje 'dat de top van een tetraeder precies boven het midden van de onderste gelijkzijdige driehoek ligt' heb ik vertaald naar die hoek van 30°. (Denk daar maar eens over na!).

Omdat een driehoek met hoeken van 30°, 60° en 90° heel bijzonder is (de schuine zijde is 2 keer zo lang als de kleinste rechthoekzijde), zou de rest van de opgave geen probleem meer mogen zijn.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 16 oktober 2003