WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Differentieerbaar in x=0

Oké, ik heb een probleempje waar ik graag wat advies bij zou kunnen gebruiken. Ik heb een functie f(x), gegeven door x=0 en f(x)=x²·sin(¹/_x). De vraag is dus of x differentieerbaar is in 0.

Wat ik dus moet doen is aantonen dat de lim_x®0f(x)=f(0)=0. Ik blijf echter steeds struikelen over de ¹/_x. Kan iemand mij vertellen hoe ik dit moet bewijzen?
Stepha
Student universiteit - donderdag 9 oktober 2003

Antwoord

De vereiste die je geeft is die voor continuiteit in x=0, niet die voor differentieerbaarheid.

De functie f(x) is trouwens niet gedefinieerd in x=0, zodat je bezwaarlijk uitspraken kan doen over de differentieerbaarheid in dat punt.

Bekijk eerst de functie f1(x)=sin(1/x)

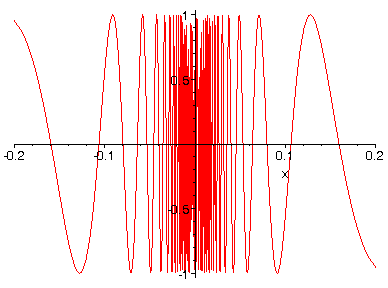
Aangezien 1/x sneller en sneller stijgt naarmate x in de buurt van nul komt, gaat de sin(1/x) sneller en sneller oscilleren. In elke omgeving van x=0 bereikt sin(1/x) de waarde a (-1a1) oneindig veel keer. De functie heeft dus geen limiet voor x=0.

Je kan de functiedefinitie dus wel uitbreiden door f1(0) een of andere waarde toe te kennen, maar welke waarde je ook kiest, je zal f1(x) niet continu kunnen maken in x=0. En een functie die niet continu is kan ook niet differentieerbaar zijn (zie je theorie)

Een nieuwe functie is f2(x)=x sin(1/x)

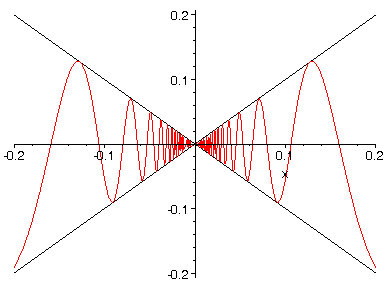
Je herkent de vorige functie, alleen wordt de amplitude van de oscillatie nu bepaald door de factor x. De functie wordt als het ware door het gaatje (0,0) geknepen.

Ook deze functie bestaat niet voor x=0. Maar aangezien

lim{x-0} x sin(1/x)
= lim{x-0} sin(1/x) / (1/x)
= lim{t-¥} sin(t)/t
= 0 (aangezien -1sin(t)+1)

kunnen we door f2(0)=0 te *definieren*, de functie continu maken in x=0. Maar is ze er ook differentieerbaar?

De definitie van differentieerbaarheid eist het bestaan van de limiet

lim{h-0} (1/h)(f(x+h)-f(x))

of in ons geval, met x=0,

lim{h-0} (1/h)(h.sin(1/h)-0)
= lim{h-0} sin(1/h}

en zoals we al aangaven bestaat die limiet niet. f2(x) is dus niet differentieerbaar in x=0.

En nu jouw functie, f3(x) = x² sin(1/x)

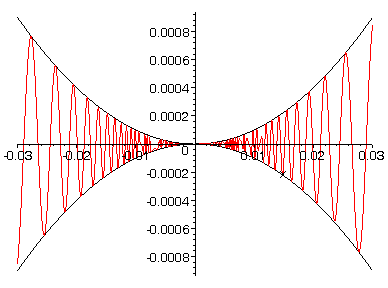
Ook hier is f3(0)=0 de enige manier om de functie continu te maken. De differentieerbaarheid vereist dan dat

lim{h-0}(1/h)(h².sin(1/h) - 0)
= lim{h-0}h.sin(1/h)

bestaat, en dat hebben we al aangetoond (zie boven, resultaat = 0).

De functie is dus afleidbaar in geheel en in het bijzonder is de afgeleide in x=0 gelijk aan 0. Hieronder zie je het verloop van de afgeleide in de buurt van x=0

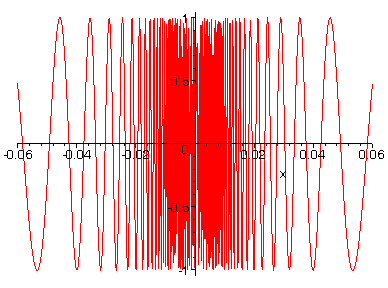
Die functie, die voor x¹0, gegeven wordt door f3'(x)=2 x sin(1/x) - cos(1/x), lijkt sterk op de functie f1(x), en ook hier kan je eenvoudig bewijzen dat de limiet voor x-0 niet bestaat.

Wat krijgen we nu? Eerst zeg ik dat de afgeleide in x=0 bestaat en gelijk is aan nul, en als ik de afgeleide bereken en x naar nul laat gaat, dan bestaat de limiet niet?!?

Volstrekt normaal. Het is niet omdat de afgeleide van een functie bestaat, dat die afgeleide op zich continu moet zijn. We zitten hier in een situatie waar

lim{x-0} f3'(x) "¹" f3'(0)
(met aanhalingstekens omdat het linkerlid niet bestaat)

Bovenstaande relatie drukt gewoon uit dat de functie f3'(x) niet continu is in x=0, maar niemand die een reden kan bedenken waarom dat had gemoeten.

Voor functies x^ksin(1/x) met k groter dan 2, zal dat wel zo zijn. Door k te verhogen dwing je de functie zich te gedragen als ze in de buurt van x=0 komt, tegen de ondeugendheid van sin(1/x) in...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 12 oktober 2003