WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Transportproblemen

Dit is een reactie op vraag 14971

maar wat bedoelt men dan met dit?
dan vraag b: Bereken door middel lineair programmeren een transportschema waarbij de transportkosten minimaal zijn?
Dan zie ik bij mijn uitwerkingen een vaag grafiekje wat er zo uitziet:
q 0 1 2 3 4 5 6 7 8...
Tk 70 151,2 199,6
Mk 81,2 48,4 22,8

Waar halen ze die q vandaan?
Lonnek
Leerling bovenbouw havo-vwo - dinsdag 7 oktober 2003

Antwoord

Ik weet eerlijk gezegd ook niet wat daarmee bedoeld wordt.
Ik neem aan dat je weet hoe je een lineair programmeringsprobleem grafisch oplost, dus met tekenen van het toegelaten gebied, en snijpunten van lijnen die bepaald worden door de ongelijkheden.
In jouw geval krijg je dit plaatje:

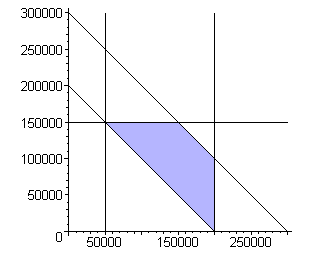
Je doelfunctie wordt: 10x - 5y + 10700000
Deze zal minimaal worden in het punt x = 50000, y = 150000.

Hopelijk heb je hier wat aan.

NB. Van collega-beantwoorder Tom kreeg ik de volgende informatie:

Hoe men aan die cijfers komt is een economisch probleem. q staat traditioneel voor de hoeveelheid (0 - 8, waarschijnlijk in een veelvoud van 100.000). De rij daaronder TK zijn de totale kosten (in dit geval gelijk aan de transportkosten). De bijhorende waarden vindt men door eerst de TK-functie op te stellen (hier normaal de doelfunctie) en dan steeds de waarde van q in te vullen bij de onbekende. Nu: hier is er een probleem want we hebben 2 onbekenden. De beste oplossing is om er 1 variabele van te maken (de totale hoeveelheid q = x + y). Maar dan komen we nog niet aan de gegevens zo te zien. Voor q = 0 hebben we 107x10^5 en niet 70. Maar dat zou ik eerst zelf eens helemaal moeten uitwerken. Misschien ook een cruciaal 'economisch' gegeven dat ontbreekt.

De laatste rij MK is steeds het verschil tussen 2 waarden van TK (of de afgeleide van TK). Economisch gezien heeft dat een invloed om de juiste hoeveelheid te kiezen. vb bepaalde mogelijke uitkomsten via LP kunnen dan al uitgesloten worden.

groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 7 oktober 2003