WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Collineaire punten

In welke bewijzen/stellingen worden collineaire punten gebruikt of komen ze in ieder geval voor.
Snippe
Leerling bovenbouw havo-vwo - donderdag 2 oktober 2003

Antwoord

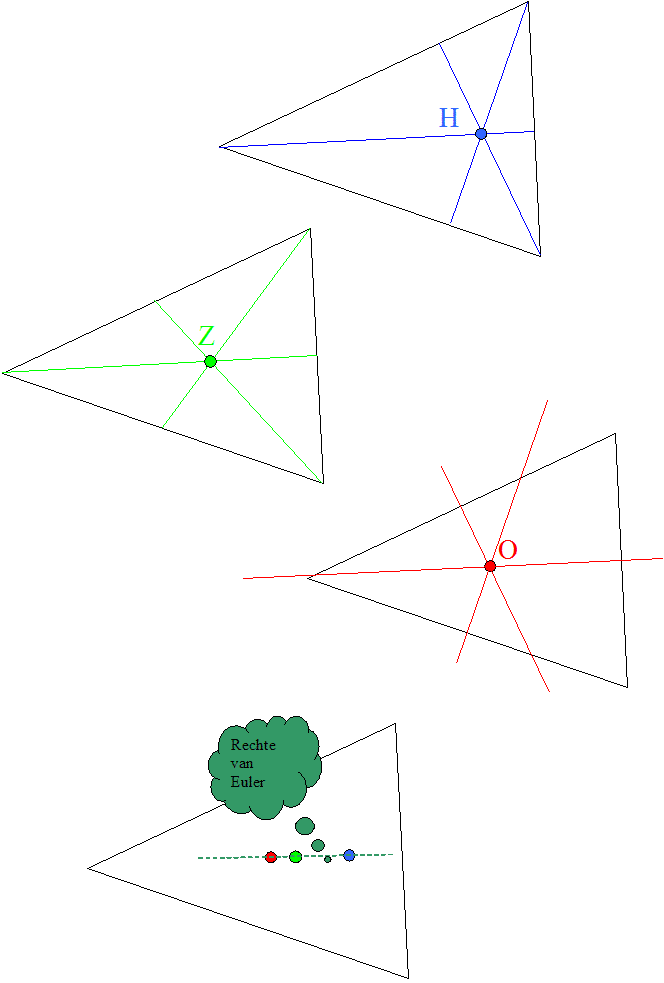
De rechte van Euler is zo'n rechte.

Voor elke driehoek geldt dat het hoogtepunt (H), het zwaartepunt (Z) en het middelpunt van de omgeschreven cirkel (O) op deze lijn liggen.

Bovendien geldt HZ:ZO = 2:1

Misschien weet je niet meer precies wat die drie punten nu precies zijn, daarom hieronder uitleg.

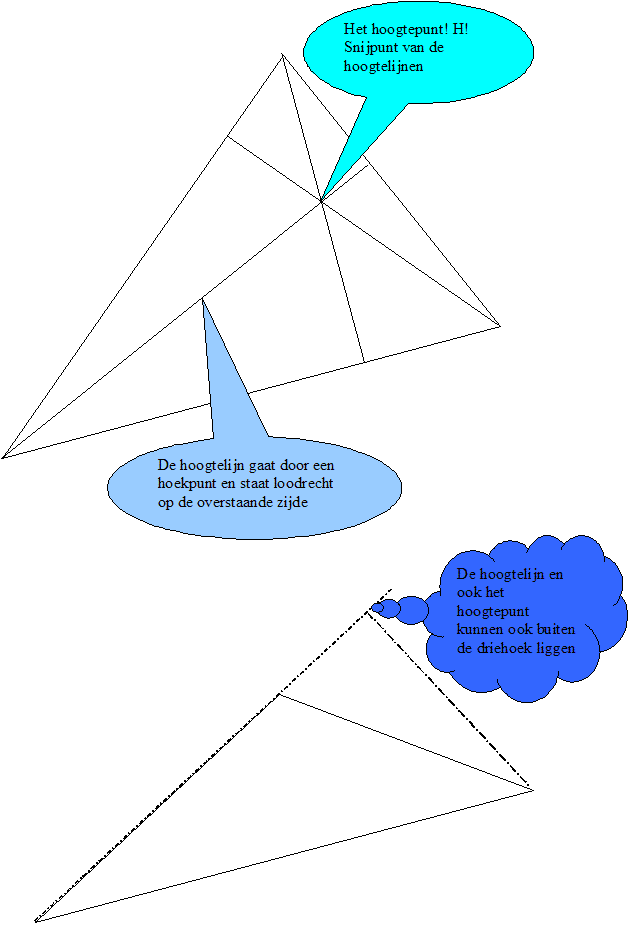
Het hoogtepunt
Het hoogtepunt is het gemeenschappelijke snijpunt van de 3 hoogtelijnen van de driehoek.
Een hoogtelijn is het lijnstuk dat een hoek loodrecht verbindt met de tegenoverliggende zijde of het verlengde daarvan.
De drie hoogtelijnen van de driehoek gaan dus door 1 punt!!

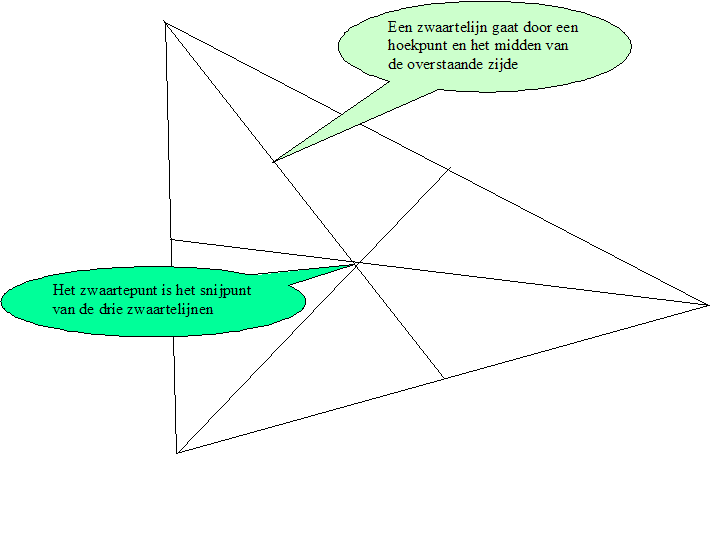
Het zwaartepunt
Het zwaartepunt is het snijpunt van de drie zwaartelijnen van de driehoek. Ze gaan wederom allemaal door hetzelfde punt.
Een zwaartelijn in een driehoek verbindt een hoekpunt met het midden van de overstaande zijde. Het zwaartepunt verdeelt ieder zwaartelijnstuk in twee delen met een verhouding 2:1. (Het langste stuk ligt aan de kant van het hoekpunt.)

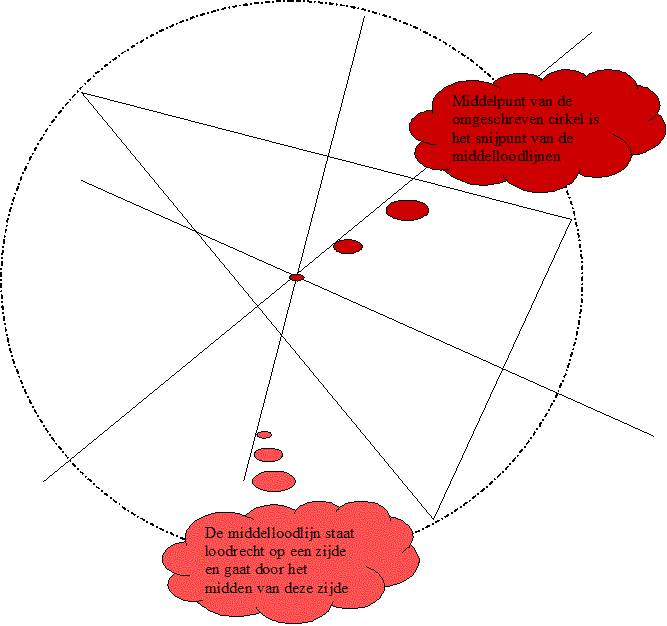
Het middelpunt van de omgeschreven cirkel
De omgeschreven cirkel gaat door de drie hoekpunten van de cirkel.
Op een cirkel hebben alle punten dezelfde afstand tot het middelpunt. Het middelpunt van de omgeschreven cirkel heeft dus dezelfde afstand tot alledrie de hoekpunten.
Het middelpunt van de omgeschreven cirkel is dan ook het snijpunt van de drie middelloodlijnen van de zijden van de driehoek.
Immers zo'n middelloodlijn is de verzameling van alle punten die even ver van twee punten liggen (in dit geval twee hoekpunten)

Rechte van Euler
Hieronder dan de constructie van de rechte van Euler!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 2 oktober 2003