|
|
|
\require{AMSmath}



Ongelijkheden
Hallo, ik heb twee vragen.
Vraag 1:
De meeste ongelijkheden snap ik, maar bij deze kom ik niet uit:
a) (1/x) (1/3) (1/3)
b) 3 + (1/(2x-1))  0 0
Ik zou het fijn vinden als u mij liet zien hoe je deze ongelijkheden zonder een plot oplost.
Vraag 2:
Langs drie zijden van een grasveld wordt een bloemperk aangelegd. Voor het geheel is een ruimte beschikbaar van 25 bij 40 meter.
Ik ben er achtergekomen dat oppervlakte van grasveld
(40-2x)*(25-x)is.
Nu de vraag:
a)Hoe groot mag de breedte van het bloemperk zijn als het grasvld minstens 400 m2 moet zijn ?
b)Bij welke breedte van het bloemperk is de oppervlakte van het bloemperk kleiner dan die van het grasveld ?
Hier kwam ik dus niet uit. Kunt u me hierbij helpen?
Alvast bedankt.
MVG
H.
H.
Leerling bovenbouw havo-vwo - woensdag 1 oktober 2003
Antwoord
Hallo H,
vraag 1
a. oplossing zonder gebruik te maken van de mogelijkheden om de grafiek te plotten.
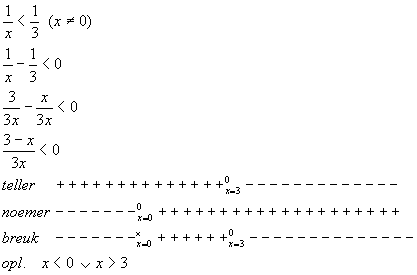
b. deze opgave kun je op dezelfde manier oplossen (voorwaarde noemer x ¹1/2)
vraag 2
Extra voorwaarde 0  x x  25 (anders is er geen gras meer) 25 (anders is er geen gras meer)
Toepassingen mag je altijd grafisch oplossen. Als dit niet zo is dan moet dat duidelijk in de opgave aangegeven zijn.
(a)
Y1 = (40-2X)(25-X)
Y2 = 400
Venster [0,25] ´ [0,1000]
Optie intersect gebruiken om de grenswaarde van x te bepalen.
Uit de grafiek volgt dan dat x 8,1 meter 8,1 meter
(b)
Opp bloemperk + Opp grasveld = 1000 m2
Opp bloemperk  Opp grasveld als Opp grasveld Opp grasveld als Opp grasveld  500® Y2 = 500 500® Y2 = 500
Of een formule opstellen voor de opp van het bloemperk ( Y2 = -2X^2 + 90X)
Y2  Y1 grafisch oplossen. Y1 grafisch oplossen.
Opmerking: de formule voor de oppervakte van het grasveld kan ook zijn:
O(x) = (40-x)(25-2x) (langs een korte zijde komt dan geen bloemperk)
wl
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 2 oktober 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 (1/3)
(1/3)  0
0 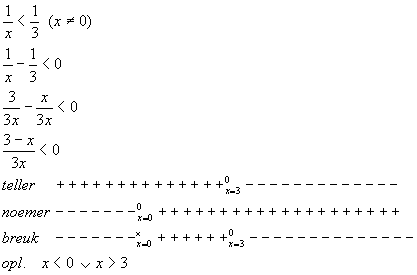
 8,1 meter
8,1 meter 