WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Constructie driehoek

Dit is een reactie op vraag 13567

CONSTRUCTIE DRIEHOEK: ( voor verduidelijking )

Gegeven zijn: de lengte van zijde a, de lengte van zijde b en de lengte van de deellijn (dc) van hoek C. ( dus de grootte van hoek C, de hoek die zijde a en zijde b maken is niet gegeven )
(AB=c, BC=a en AC=b )
Te berekenen is zijde c wel met de volgende formules:
(die zijn in de vlakke meetkunde bekend of althans af te leiden)
* is het maalteken (x)

1)
dc*dc = a*b - p*q ( p en q zij de delen van zijde c die door dc afgesneden worden ( dus p+q = c )
2)
p = a*c/(a+b) en q = b*c/(a+b)
formule van 1) wordt dan:

dc*dc = a*b - (a*b*c*c)/[(a+b)(a+b)]

hieruit volgt c en daaruit weer driehoek ABC, want de drie zijden zijn dan bekend. ( uiteraard kan c op deze manier ook geconstrueerd worden)
Maar zou driehoek ABC met liniaal en passer te construeren zijn met bovenvermelde gegevens.(dus op een andere wijze )
Dat was eigenlijk mijn vraag. (misschien een moeilijke vraag )
Bij voorbaat hartelijk dank

J. Vri
Iets anders - zaterdag 20 september 2003

Antwoord

Inderdaad niet gemakkelijk, maar wel leuk!
Je zou het volgende kunnen doen.
Jouw formule kun je omschrijven tot:
c² = (a + b)² - (a + b)²·dc²/(a·b)
construeer nu x = a + b
De formule wordt dan:
c² = x² - x²·dc²/(a·b)
construeer vervolgens y zodat y/x = dc/a (zie plaatje)

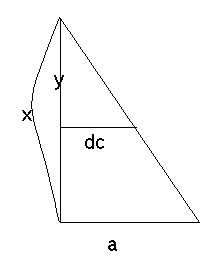
Op vergelijkbare manier kun je z construeren zodat z/x = dc/b
De formule wordt dan:
c² = x² - y·z
Nu moet je nog een constructie bedenken voor een lengte u zodat u² = y·z, en dan kun je met Pythagoras uiteindelijk c construeren. Lukt dat?

NB. Van collega-beantwoorder Dick kreeg ik nog een mooie meetkundige constructie toegestuurd.
Aannemend dat we driehoek ABC hebben...
Daarin zijn dus gegeven BC = a, CA = b en CP = d (de lengte van de bissectrice van C).

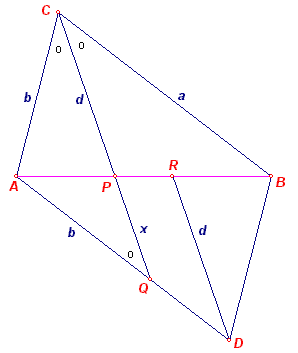
Vorm uit ABC het parallellogram ADBC, met verder Q het snijpunt van CP en AD en DR//CQ (R op AB).
Daaruit volgen dan de in de tekening aangegeven lengtes van enkele andere lijnstukken; ook is AD = a.
Stel PQ = x.
Uit ADR ~ AQP volgt dan AD : AQ = DR : QP of ook a : b = d : x
PQ is dus als vierde evenredige te construeren bij a, b en d.
Hiermee is driehoek AQC te construeren (ZZZ).
En dan vinden we eenvoudig P op CQ en B als snijpunt van de lijn AP met de cirkel (C, a).

Om het nog mooier te maken: hier nog een bijdrage van Dick met volgens ons de eenvoudigste constructie:
In de figuur is BD//CP

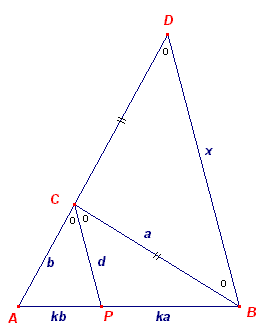
Noem BD = x
Volgens de bissectricestelling is nu AP=k·b en BP=k·a
Dan is CP:DB = AP:AB = b:(b+a)
dus d:x = b:(b+a), waarmee x te construeren is uit a, b en d.
Dus driehoek BDC is te construeren, verleng DC met b (geeft A), trek AB en klaar!

Dick kan er geen genoeg van krijgen, dus hier nog een mooie constructie:
Kijk eens naar onderstaande figuur, waarin de volgende cirkels zijn getekend: (C, a), (C, b) en (C, d).

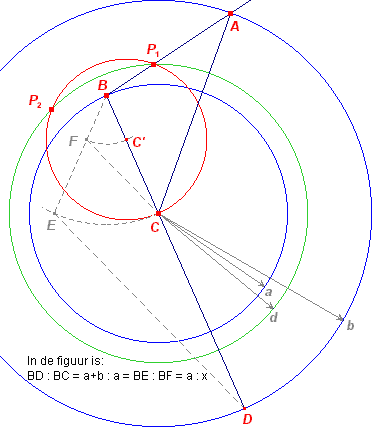
Kies voor de constructie alvast het punt B willekeurig op cirkel (C, a).
En dan nu ervan uitgaande dat we ABC reeds hebben…
P (in de figuur P₁) ligt zo op AB, dat AP : BP = b : a (bissectricestelling).
P is dus het beeld van A bij een vermenigvuldiging uit B met de factor a/(a + b).
Maar A ligt op de cirkel (C, b).
P ligt dan dus op een cirkel die het beeld is van (C, b) bij vermenigvuldiging uit B met genoemde factor.
Die beeldcirkel gaat door C, immers BC = a en BD = a + b; C is dan het beeld van D.
Het middelpunt C' van bedoelde beeldcirkel laat zich eenvoudig uit het punt C construeren met de in de figuur staande evenredigheid (waarbij x = BF = BC').
Maar P ligt ook op de cirkel (C, d).
Het punt P is dus één van beide snijpunten van de cirkels (C', C'C) en (C, d).
Trek dan BP, die (C, b) in A snijdt, en we hebben de driehoek!

succes,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 21 september 2003