WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Tekenen van complexe functies (2)

Dit is een reactie op vraag 13908

Nog een PO'er :-).
Ok, onderhand denk ik dat ik hem wel doorheb. Alleen als ik dit uit wil werken dan is het een beetje moeilijk om te beschrijven hoe het nou allemaal precies zit met die figuren. Want ik weet dat bijvoorbeeld met de 'eenheidscirkel' (straal 1 en i) dan met die functie gespiegeld wordt in de x-as. Een rechte lijn door de oorsprong wordt gespiegeld in de i-as, enz enz.

Nu probeer ik te bedenken hoe ik de coordinaten van twee cirkels die niet hun centrum in de oorsprong hebben, om die dan in te voeren in de 1/z en dan te vergelijken en daar mijn conclusie uit te halen. Maar ik loop een beetje vast op die coordinaten.

Hebben jullie misschien suggesties voor coordinaten van twee cirkels die ik kan gebruiken? En verder bedankt voor alle antwoorden op onze vragen tot nu toe :-).
Groetjes

Er stond hier onder een tabel waarin alle invoer en uitvoer van de eenheidscirkel stond ingevuld vanuit die functie 1/z, maar de tekens werken niet mee, dus jullie zullen me helaas op mn woord moeten geloven dat ik het wel snap
Kevin
Leerling bovenbouw havo-vwo - donderdag 18 september 2003

Antwoord

Ik geloof je op je woord, wat betreft die eenheidscirkel!

En dan nog even iets over die rechte lijnen door O. Er is eigenlijk sprake van méér dan een spiegeling in de r-as (reële as), of toch de i-as (imaginaire as), zoals jij schrijft.

Kijk nog eens naar de applet Tekenen van complexe functies en beweeg (als het punt P samenvalt met O) het punt A over de lijn.

Als A buiten de eenheidscirkel ligt, dan ligt A' erbinnen, en omgekeerd!

Tja, en dan die willekeurige cirkels.
Je hebt gezien dat ze in het algemeen worden afgebeeld op cirkels. Als zo'n cirkel door O gaat, dan is het beeld een rechte lijn.
Manipulatie met complexe getallen is in dit geval wat ingewikkeld.

Daarom is het het handigst op zo'n cirkel DRIE punten te kiezen (bij een cirkel door O twee) en daarvan het beeld bij de afbeelding w = 1/z te bepalen (op dezelfde manier als je dat -vermoedelijk- met punten van de eenheidscirkel hebt gedaan).

Zie onderstaand plaatje, waarin cirkels met middelpunt M(1,1) zijn getekend, met straal √2 (die gaat door O) en straal 2.

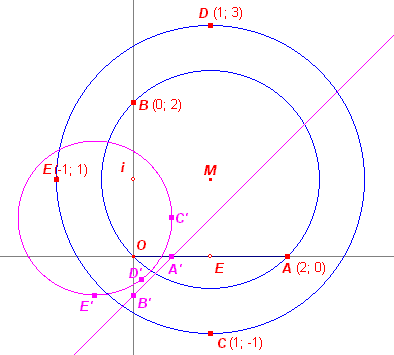
Probeer nu zelf eens de coördinaten van de punten A', B', C', D' en E' te vinden.

Als je de coördinaten hebt, dan heb je natuurlijk ook de bijbehorende complexe getallen (omgekeerd natuurlijk)...
Dan rest je bij de laatste cirkel ook nog de coördinaten van het middelpunt van die cirkel te vinden! En als je dat middelpunt hebt, dan heb je natuurlijk ook de straal van die beeldcirkel.

Opmerking: dat middelpunt is NIET het beeld van het punt M!

Succes.
En als 't niet lukt, je weet ons te vinden...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 18 september 2003