'F' en 'Z' hoeken komen voor als je ergens twee evenwijdige lijnen hebt.

Als deze twee evenwijdige lijnen door een derde lijn worden gesneden krijg je de volgende figuur:
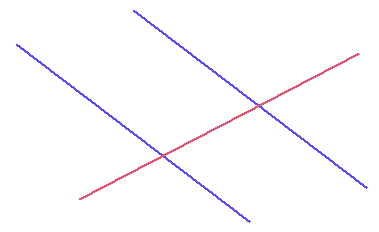
In bovenstaande figuur kan je (met een beetje moeite) allerlei 'F'-figuren ontdekken. Daarbij lopen de twee streepje van de 'F' steeds evenwijdig:
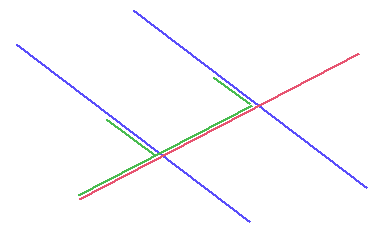
Als je zo'n 'F'-figuur ziet dan weet je dat de twee hoeken (met de rode rondjes) gelijk zijn!
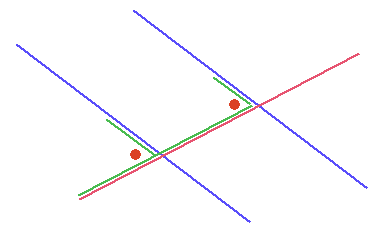
Maar er zijn natuurlijk nog meer 'F'-figuren te ontdekken:
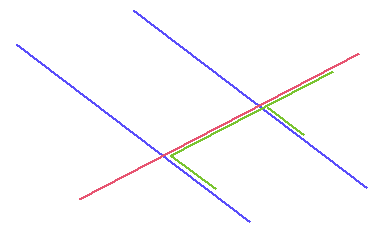
En ook hier zijn er weer twee hoeken gelijk:
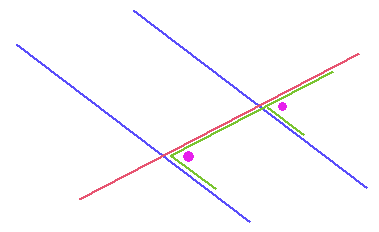
In de figuur met de twee evenwijdige lijnen en een derde lijn kan je ook 'Z'-figuren ontdekken. Hierbij lopen ook twee streepjes van de 'Z' steeds evenwijdig:
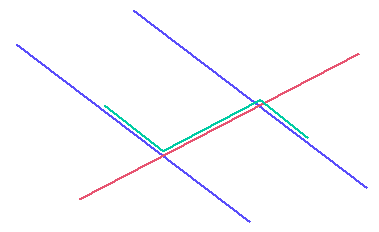
In dat geval weet je ook dan de twee 'binnenhoeken' gelijk zijn:
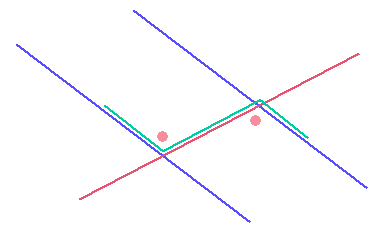
Maar ook hier kan je verschillende 'Z'-figuren ontdekken...
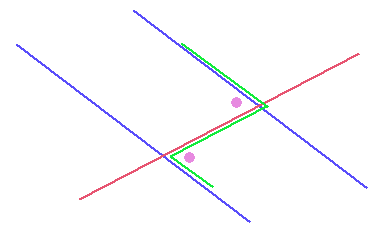
Een voorbeeld:
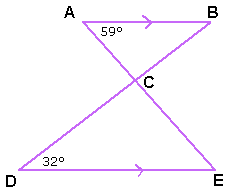
Er is gegeven dat AB evenwijdig is aan DE. (Aha, misschien moet ik wel iets met 'F'-hoeken of 'Z'-hoeken doen!)
 A=
A= E (Waarom?)
E (Waarom?)
Dus  E is ook 59 graden.
E is ook 59 graden.Nog een voorbeeld:
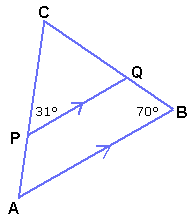
Hier is PQ evenwijdig aan AB (Aha, misschien...).  CPQ=
CPQ= A (Waarom?)
A (Waarom?)
En zo zit dat... hopelijk heb je er iets aan!


















 A=
A=

