WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Numerieke analyse

Gegeven:y=ln(x)-1-1/x
1.Geef een lokatie van het(de) nulpunt(en) van deze functie.
2.Bereken het grootste nulpunt tot 6 cijfers nauwkeurig met de methode van Newton Raphson
3.Bereken het kleinste nulpunt tot 4 cijfers nauwkeurig met de successieve substitutie methode.
4.Leg de successieve substitutiemethode grafisch uit.

volgens mij heeft die ma 1 nulpunt, en hoe kunt ge verschil leggen in kleinste en grootste nulpunt in de formules van de substitutie methodes.
alvast bedankt!
Jimmy
Student Hoger Onderwijs België - zaterdag 30 augustus 2003

Antwoord

1) Bereken de afgeleide van deze functie eens. Bekijk deze afgeleide op het domein dan kun je makkelijk inzien dat er maar een nulpunt kan zijn. Door wat in te vullen kan je makkelijk zien dat dat nulpunt tussen de 3 en de 4 moet liggen, dat zal hier ook wel de bedoeling zijn.

2) Het principe van de methode Newton Raphson kun je terugvinden bij de beantwoorde vragen, daar wordt alles haarfijn uitgelegd.

3) Bij de methode van successieve substitutie moet je de vergelijking f(x)=0 omwerken in een vergelijking van de vorm x=g(x), dat kan hier op zeker drie verschillende manieren. Daarbij moet je wel zoeken naar die manier waarbij de methode van successieve substitutie convergeert. Dat is alleen het geval indien in de buurt van het snijpunt geldt dat |g'(x)|1. De consequentie is dat dus niet elke omwerking van f(x)=0 naar x=g(x) zal werken.
In dit geval kun je f(x)=ln(x)-1-1/x=0 omwerken tot x=e^1+1/x (ga na).
De situatie die je dan krijgt staat in de onderstaande figuur:

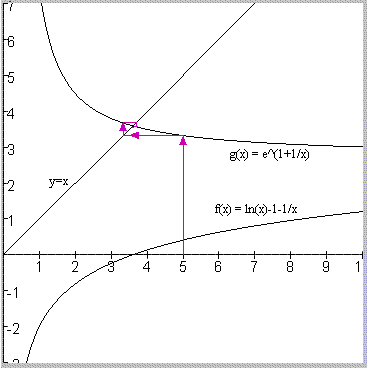
Wat er nu gebeurt kun wel je zien. Begin met schatting x=5 voor het snijpunt dan krijg je de volgende rij van schattingen door telkens de uitkomst weer in te vullen in e^1+1/x:
5®3,32®3,6737®3,5687®3,5974®3,5894®3,5916®3,5910®
3,5912
De werkelijk oplossing zit in dit geval telkens tussen twee opeenvolgende schattingen in dus je weet nu dat de oplossing 3,591 is (in 3 decimalen achter de komma nauwkeurig). Voor dat 4^e decimaal moet je nog even verder gaan (zelf doen !)
Er is ook nog wel een formule waarmee je schattingsfout/ convergentiesnelheid kunt berekenen, maar dat gaat misschien wat ver en in is hier niet nodig.
Nog even wat losse eindjes aan elkaar knopen en je oplossing is klaar.

Met vriendelijke groet

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 30 augustus 2003