WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hotelporselein

Hallo ben een meisje van 17 jaar en kreeg volgende vraag voorgeschoteld op mijn examen aangezien ik niet slaagde moet ik herexamens doen en waarschijnlijk zal er weer zo een vraag tussen zitten, kunnen jullie mij helpen?

In een fabriek word hotelporselein vervaardigd. Er zijn 3 controle beurten bij de eerste controlebeurt word de vorm bekeken: 25% voldoet niet aan de gestelde norm. Bij de 2e controle is de kleur aan de beurt: 85% voldoet.. bij de 3e controle word op fouten opgespoord: nu voldoet 80%

Alle porselein dat de 3 controlebeurten gunstig doorstaat word verkocht als eerste keus. Is slechts 1 van de controles negatief dan hebben we 2e keus. Porselein met slechts 1 positieve controle word tegen een prikje verkocht als 3e keus. De rest wordt meteen vernietigd.als men willekeurig een stuk porselein kiest, hoe groot is de kans dat het
a. derde keus is
b. vernietigd zal worden

Toch moeilijk, niet?
xxx
Suma
3de graad ASO - zaterdag 30 augustus 2003

Antwoord

Om een goed 'beeld' te krijgen van de situatie kan je eerst een kansdiagram (stroomdiagram) maken:

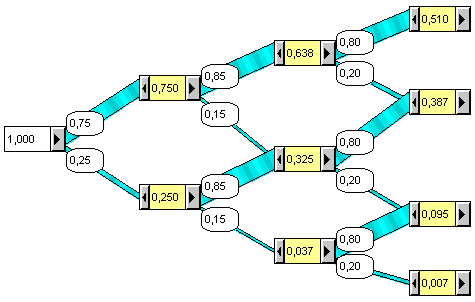
Omhoog betekent een positieve controle, naar beneden negatief. In het bovenstaande (verkort) diagram kan je de kansen al aflezen. Maar we gaan ze ook berekenen....

Wat is de kans op derde keus?
Om een derde keus te worden moeten er twee controles negatief uitvallen.
Dat kan op 3 manieren:
A: + - -
B: - + -
C: - - +
In het diagram komen die allemaal samen bij het vakje waar 0,095 staat.

P(A)=0,75·0,15·0,20=0,0225
P(B)=0,25·0,85·0,20=0,0425
P(C)=0,25·0,15·0,80=0,03
Totaal: 0,0225+0,0425+0,03=0,095

Wat is de kans op vernietiging?
Dat kan maar 1 manier:
V: - - -
P(V)=0,25·0,15·0,20=0,0075

...en dat viel toch best mee toch? Om te oefenen zou je eens kunnen proberen de kans op 2^e keus uit te rekenen. Het antwoord staat er al...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 30 augustus 2003